Hypothesis Test in MATLAB (codes included)

Utpal Kumar   3 minute read      

Let’s pose the null hypothesis that the two sets of data come from the same probability distribution (not necessarily Gaussian). Under the null hypothesis, the two sets of data are interchangeable, so if we aggregate the data points and randomly divide the data points into two sets, then the results should be comparable to the results obtained with the original data.

Key idea — test a claim by simulating “no effect.” A hypothesis test pits a null hypothesis $H_0$ (“the two samples come from the same population”) against an alternative. Here we test it by randomization: pool both samples, shuffle, and re-split thousands of times, each time recording the difference in means. That builds the distribution of differences you’d expect if $H_0$ were true. The p-value is the fraction of those shuffled differences at least as extreme as the one you actually observed. If $p$ is below your chosen significance level $\alpha$ (say 0.05), the observed difference is unlikely under $H_0$, so you reject it. Crucially, failing to reject $H_0$ is not proof it’s true — it may just be a Type II error.

The four outcomes of a hypothesis test A two-by-two table. Columns are the unknown truth: the null hypothesis is true, or the null hypothesis is false. Rows are your decision: reject the null, or fail to reject it. Rejecting a true null is a Type I error (false positive, rate alpha). Failing to reject a false null is a Type II error (false negative, rate beta). The other two cells are correct decisions; rejecting a false null is the test's power. The unknown truth H₀ is TRUE H₀ is FALSE Reject H₀ Fail to reject H₀ Type I error false positive rate = α Correct true positive power = 1 − β Correct true negative 1 − α Type II error false negative rate = β You pick α (the Type I rate). “Fail to reject” is not proof H₀ is true — it may be a Type II error.
The four outcomes of a hypothesis test. You set the Type I error rate α; "fail to reject" is not proof the null is true — it can be a Type II error.

So, the strategy is to generate random datasets, with replacement (bootstrapping), compute difference in means (or difference in medians or any other reliable statistic), and then compare the resulting values to the statistic computed from the original data.

Histogram of the difference-in-means from 10,000 randomizations, with a red line marking the observed difference far in the tail 
%% Hypothesis Testing
clear; close all; clc;
data1=randn(100,1);
data2=(randn(150,1).^2)*10 + 20;
all_data=[data1; data2];
  • Null hypothesis is that the two distribution that we are sampling are from the same population.
%% First Sample
mu1=mean(data1);

%% Second Sample
mu2=mean(data2);
actualdiffmn=(mu1-mu2)
  • Now, since our null hypothesis is that the two distribution comes from the same population, we can mix it to draw two samples again.
%% Using Randomization to test the hypothesis
numsim = 10000;   % number of simulations to run
mn1=zeros(1,numsim);
mn2=zeros(1,numsim);
diffmn = zeros(1,numsim);
for num=1:numsim
    % vector of indices (a random ordering of the integers between
    % 1 and n where n is the number of data points)
    indx = randperm(length(all_data));
    data_sim=all_data(indx);
    data_sim1=data_sim(1:length(data1));
    data_sim2=data_sim(1:length(data2));
    mn1(num)=mean(data_sim1);
    mn2(num)=mean(data_sim2);
    diffmn(num)=(mn1(num)-mn2(num));
end

% visualize
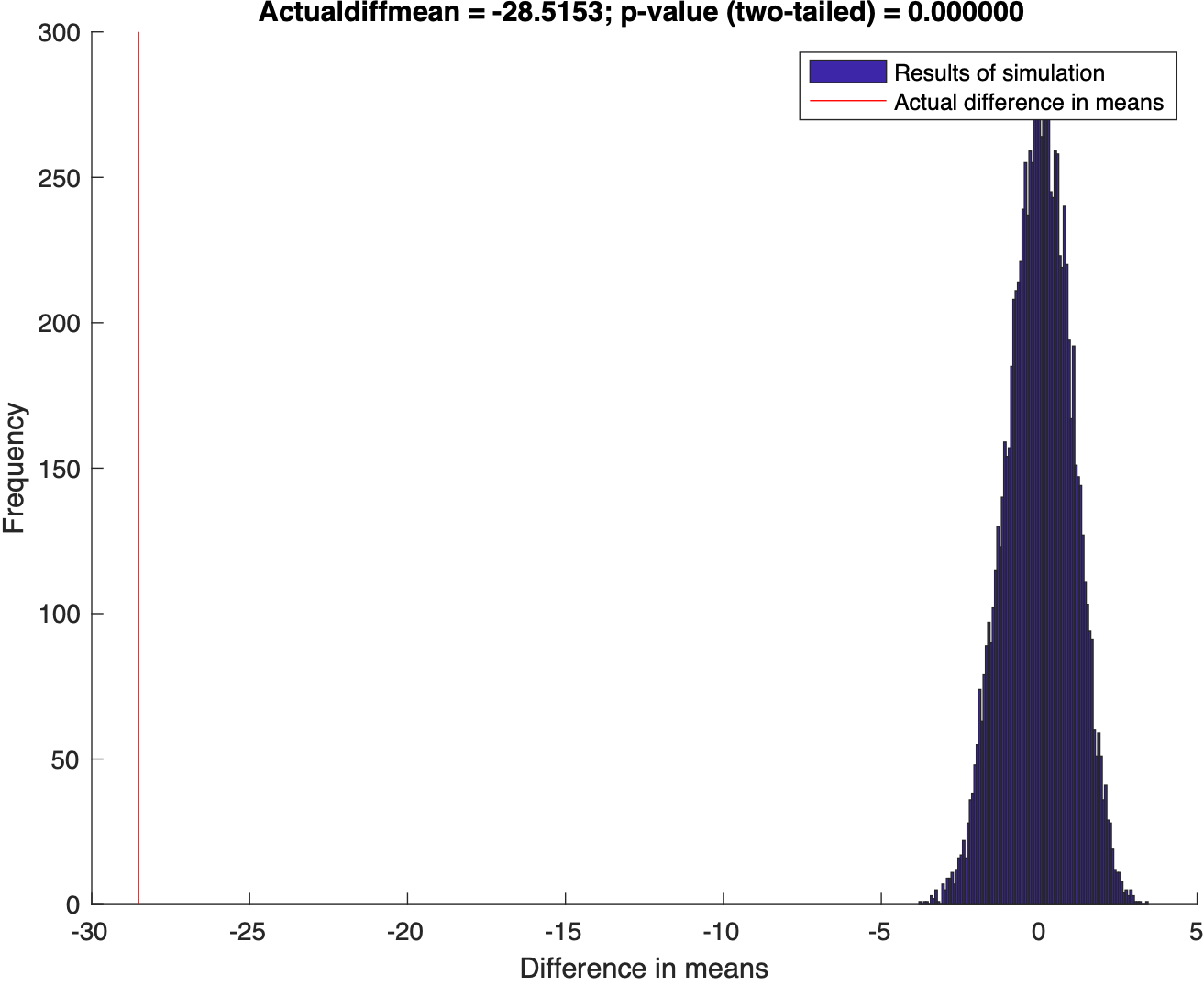
figure; hold on;
hist(diffmn,100);
ax = axis;
plot(repmat(actualdiffmn,[1 2]),ax(3:4),'r-');
pval = sum(abs(diffmn) > abs(actualdiffmn)) / length(diffmn);
title(sprintf('Actualdiffmean = %.4f; p-value (two-tailed) = %.6f',actualdiffmn,pval));
legend('Results of simulation','Actual difference in means')
xlabel('Difference in means'), ylabel('Frequency')

actualdiffmn =
  -28.5153

MATLAB note: the code uses hist(diffmn,100), which still runs but is legacy — current MATLAB recommends histogram(diffmn,100) (better default binning). The randomization logic is unchanged.

Quick check: The simulation returns a two-tailed p-value of 0.0001 for the observed difference in means. At $\alpha = 0.05$, what’s the right conclusion?

  • Accept $H_0$ — the two samples are proven identical
  • Reject $H_0$: a difference this large is very unlikely if the samples came from the same population
  • Nothing, because randomization tests can’t produce p-values
  • Re-run with fewer simulations to raise the p-value

Recap

  • State $H_0$ (here: both samples come from one population) and pick a significance level $\alpha$.
  • Randomization test: pool the data, shuffle and re-split numsim times with randperm, and record the statistic (difference in means) each time — this is the null distribution.
  • The p-value = fraction of shuffled statistics at least as extreme as the observed one (sum(abs(diffmn) > abs(actualdiffmn))/numsim).
  • Reject $H_0$ when $p < \alpha$; otherwise fail to reject — which is not the same as proving $H_0$ true (that risks a Type II error).
  • This resampling approach needs no Gaussian assumption — it works for any distribution and any statistic.

Where to go next

Disclaimer of liability

The information provided by the Earth Inversion is made available for educational purposes only.

Whilst we endeavor to keep the information up-to-date and correct. Earth Inversion makes no representations or warranties of any kind, express or implied about the completeness, accuracy, reliability, suitability or availability with respect to the website or the information, products, services or related graphics content on the website for any purpose.

UNDER NO CIRCUMSTANCE SHALL WE HAVE ANY LIABILITY TO YOU FOR ANY LOSS OR DAMAGE OF ANY KIND INCURRED AS A RESULT OF THE USE OF THE SITE OR RELIANCE ON ANY INFORMATION PROVIDED ON THE SITE. ANY RELIANCE YOU PLACED ON SUCH MATERIAL IS THEREFORE STRICTLY AT YOUR OWN RISK.

Leave a comment