Monte Carlo Simulation to test for the correlation between two dataset in MATLAB (codes included)

Monte Carlo Simulations (MCS) can be used to extract important informations from the dataset that would be impossible to assess otherwise. Using MCS rather than the traditional methods to find the relation between two datasets are more intuitive.

What is Monte Carlo Simulations??

MCS studies are computer-driven experimental investigations in which certain parameters, such as population means and standard deviations that are known a priori, are used to generate random (but plausible) sample data (Mooney 1997). These generated data are then used to evaluate the sampling behavior of one or more statistics of interest. This process of generating and analyzing data is repeated over many iterations and differing conditions that are thought to influence the sampling behavior of the statistic of interest (e.g., through increasing sample size, mean differences, variability). [3]

%%Monte Carlo simulations of correlation values
clear; close all; clc;
% define
numsim = 10000;   % number of simulations to run
samplesize = 50;  % number of data points in each sample

% pre-allocate the results vector
results = zeros(1,numsim);

% loop over simulations
for num=1:numsim

  % draw two sets of random numbers, each from the normal distribution
  data = (randn(samplesize,2).^2)*10+20;

  % compute the correlation between the two sets of numbers and store the result
  results(num) = corr(data(:,1),data(:,2));

end
% visualize the results
figure; hold on;
hist(results,100);
% ax = axis;
% mx = max(abs(ax(1:2)));  % make the x-axis symmetric around 0
% axis([-mx mx ax(3:4)]);
xlabel('Correlation value');
ylabel('Frequency');
%%
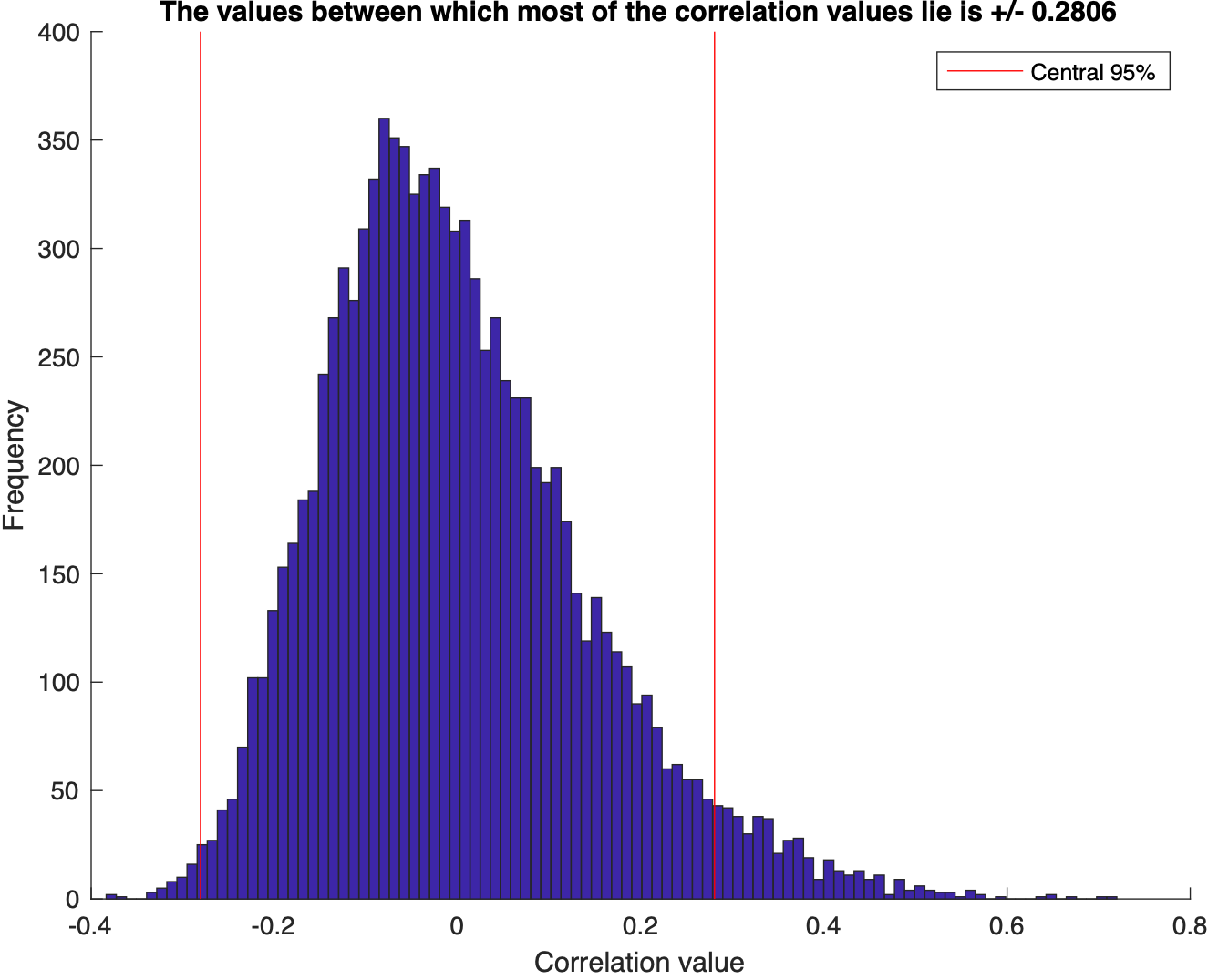
val = prctile(abs(results),95);
val
%%

% visualize this on the figure
ax = axis;
h1 = plot([val val],ax(3:4),'r-');
h2 = plot(-[val val],ax(3:4),'r-');
legend(h1,'Central 95%');
title(sprintf('The values between which most of the correlation values lie is +/- %.4f',val));
saveas(gcf,"monteCarloSim",'pdf')
%%

Recap

• Monte Carlo answers “could this pattern be chance?” by simulating chance thousands of times instead of relying on a closed-form test.
• To test a correlation: draw two independent random samples, corr them, repeat numsim times, and collect the results into a null distribution.
• prctile(abs(results),95) gives the central-95 % cutoff; a real correlation beyond it is significant at roughly the 5 % level.
• The approach generalizes to any statistic — swap corr for whatever you’re testing.
• Use histogram (not the legacy hist) to visualize the null distribution in current MATLAB.

Where to go next

• Easy statistical analysis in MATLAB — descriptive stats and the classical one-sample t-test.
• Hypothesis testing — the null/alternative framework Monte Carlo is simulating here.

References:

1. Kay, K. Lectures on Statistics and Data Analysis in MATLAB (archived).
2. Clifford, P., Richardson, S., & Hémon, D. (1989). Assessing the significance of the correlation between two spatial processes. Biometrics, 45(1), 123–134.
3. Sigal, M. J., & Chalmers, R. P. (2016). Play it again: Teaching statistics with Monte Carlo simulation. Journal of Statistics Education, 24(3), 136–156.