Time-Frequency Analysis in MATLAB (codes included)
A signal has one or more frequency components in it and can be viewed from two different standpoints: time-domain and frequency domain. In general, signals are recorded in time-domain but analyzing signals in frequency domain makes the task easier. For example, differential and convolution operations in time domain become simple algebraic operation in the frequency domain.
Introduction
Signals can be any time-varying or space-varying quantity. Examples: speech, temperature readings, seismic data, stock price fluctuations.
A signal has one or more frequency components and can be viewed from two different standpoints: time-domain and frequency domain. In general, signals are recorded in the time-domain but analyzing signals in the frequency domain makes the task easier. For example, differential and convolution operations in the time domain become simple algebraic operations in the frequency domain.
Similar posts
Fourier Transform of a signal
We can go between the time-domain and frequency-domain by using a tool called Fourier transform.
Now to get comfortable with Fourier transform, let’s take an example in MATLAB:
clear; close all; clc
%%Creating dataset
fs=100; %sampling frequency (samples/sec)
t=0:1/fs:1.5-1/fs;%time
f1=10; %frequency1
f2=20; %frequency2
f3=30; %frequency3
x=1*sin(2*pi*f1*t+0.3)+2*sin(2*pi*f2*t+0.2)+3*sin(2*pi*f3*t+0.4);
We represent the signal by the variable \( x\). It is the summation of three sinusoidal signals with different amplitude, frequency, and phase shift. We plot the signal first.
%%Visualizing data
figure(1)
plot(x)
legend('Two-tone signal')
saveas(gcf,'signal_plot.jpg')
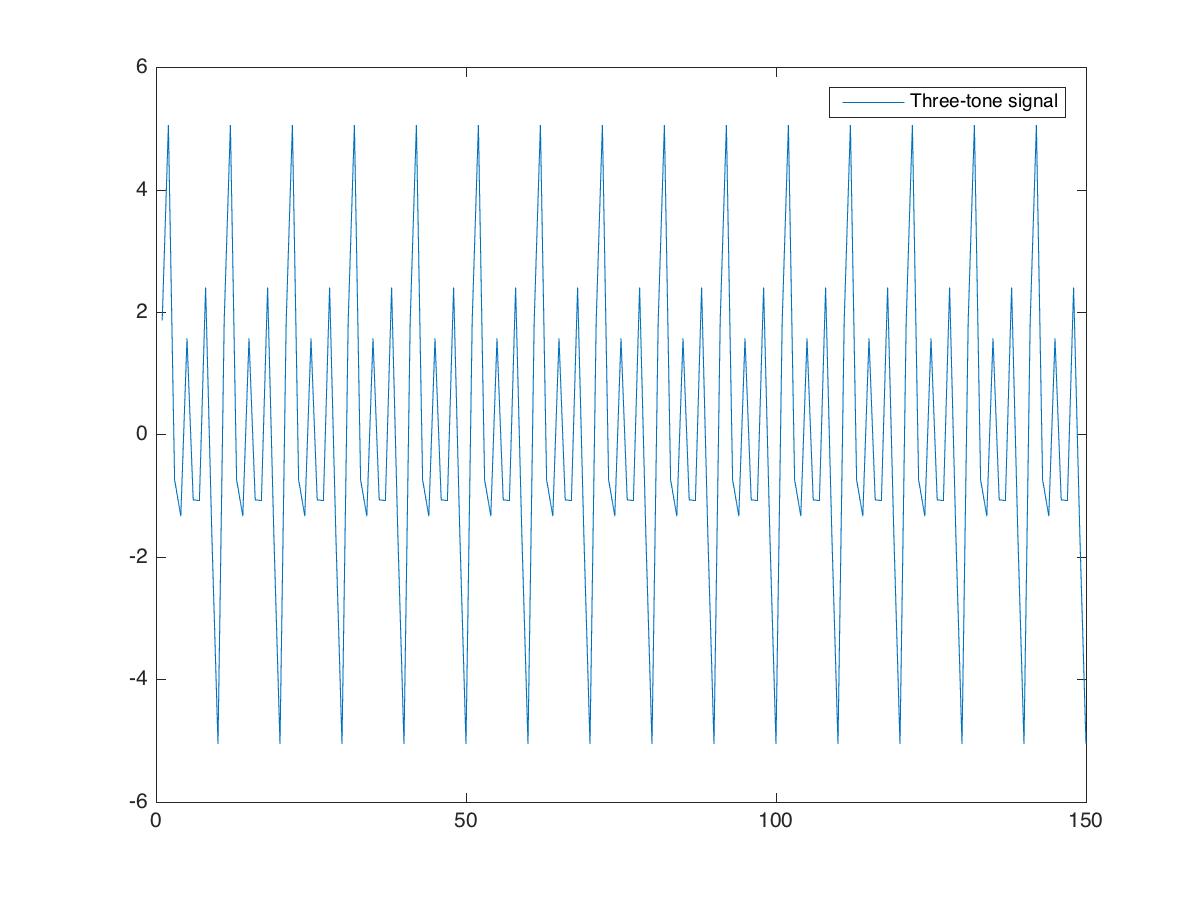
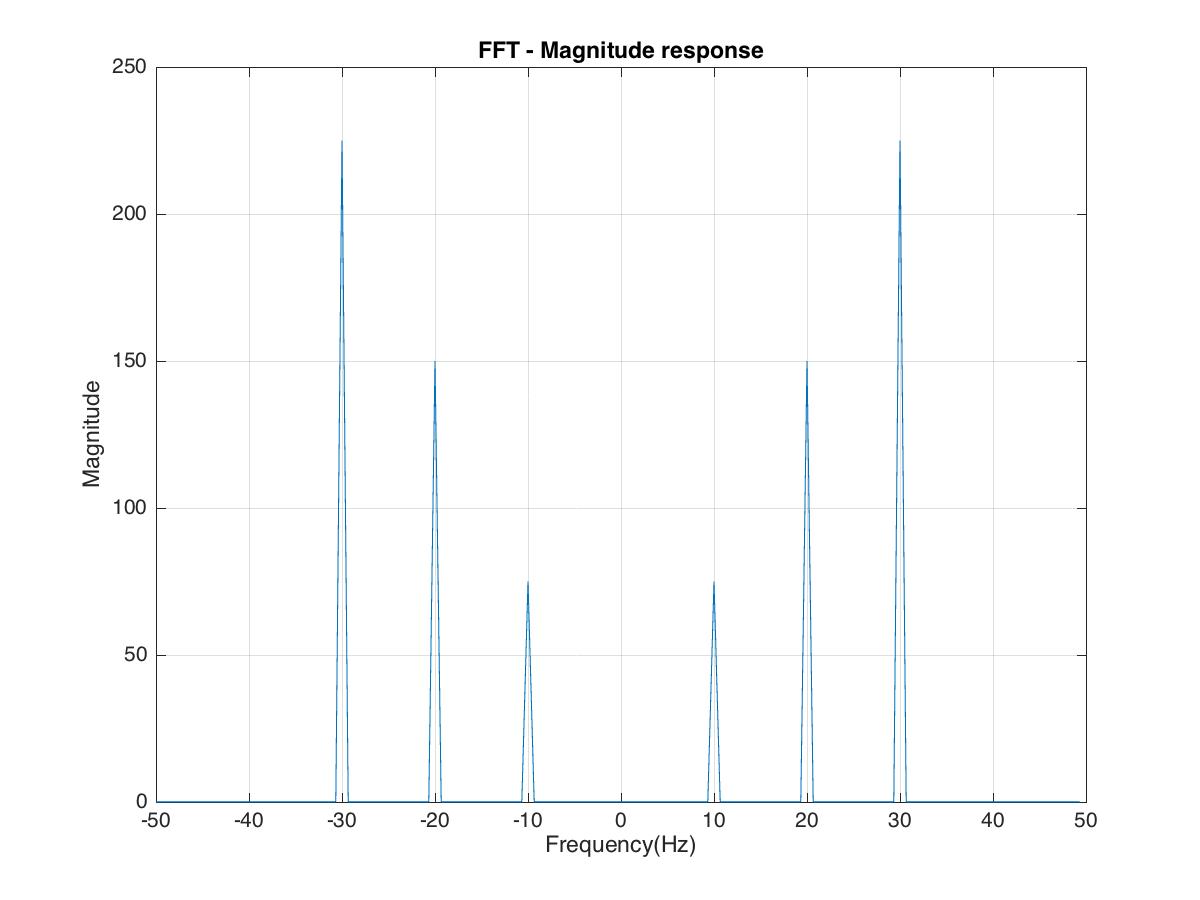
We then do the Fourier transform of the signal to obtain its magnitude and phase spectrum.
%%Fourier transform of the data
X=fft(x);
X_mag=abs(fftshift(X)); %magnitude
X_phase=angle(fftshift(X)); %phase
%%Frequency bins
N=length(x);
Fbins=(-N/2:N/2-1)/N*fs;
%%Magnitude response
figure(2);
plot(Fbins,X_mag)
xlabel('Frequency(Hz)')
ylabel('Magnitude')
title('FFT - Magnitude response')
grid on
saveas(gcf,'fft_mag_response.jpg')
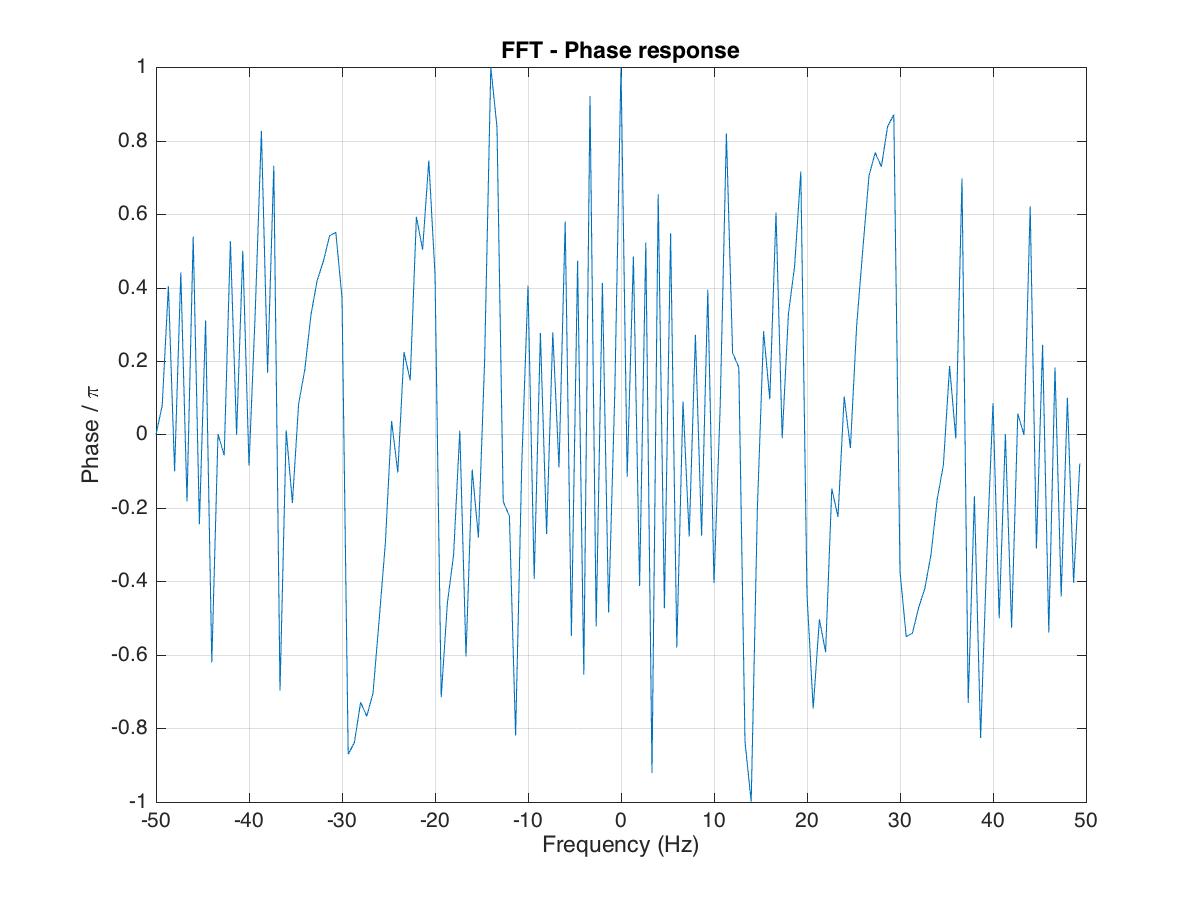
%%Phase response
figure(3);
plot(Fbins,X_phase/pi)
xlabel 'Frequency (Hz)'
ylabel 'Phase / \pi'
title('FFT - Phase response')
grid on
saveas(gcf,'fft_phase_response.jpg')
Power spectrum estimation using the Welch’s method
Now we compute the power spectrum using the Welch’s method. We can use the function “pwelch” in Matlab to obtain the desired result.
pwelch(x,[],[],[],fs) %one-sided power spectral density
saveas(gcf,'power_spectral_plot.jpg')
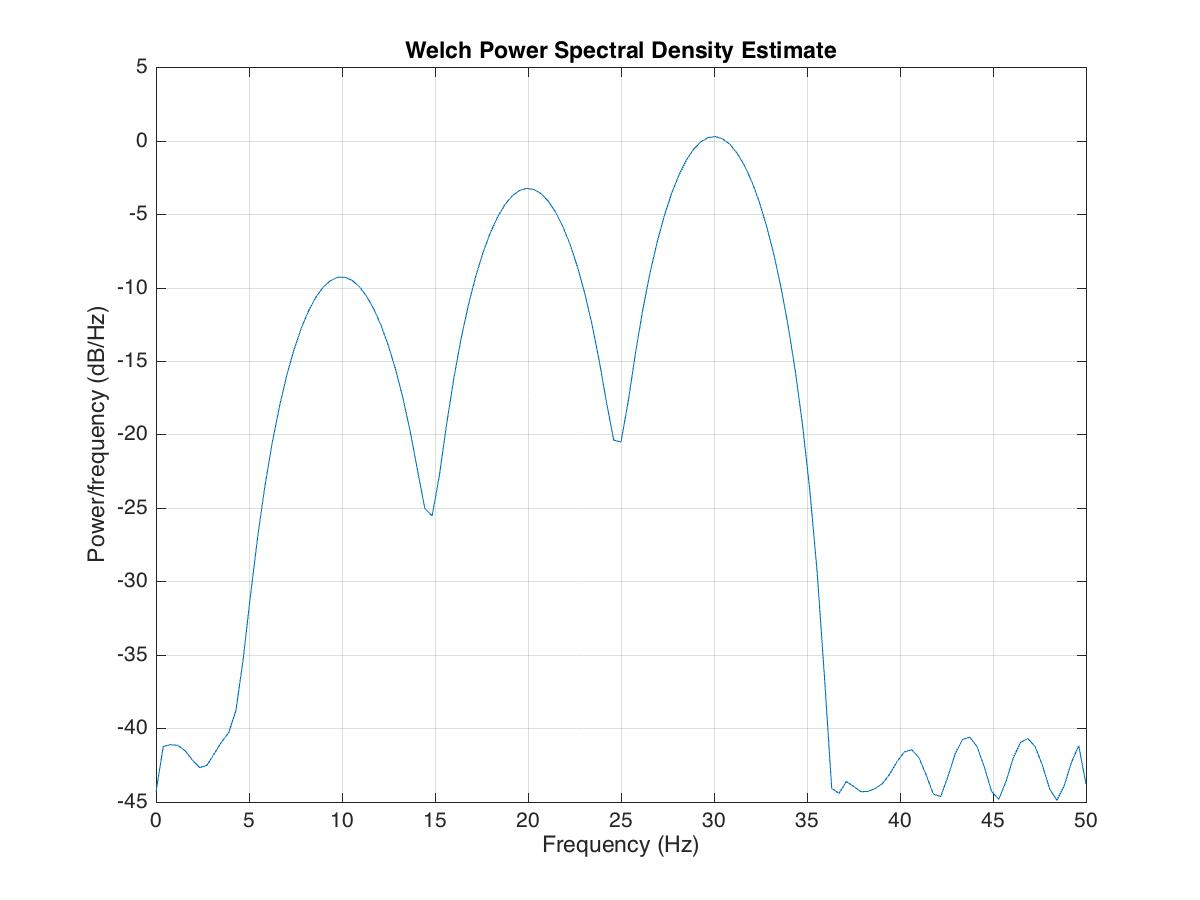
Pwelch is a spectrum estimator. It computes an averaged squared magnitude of the Fourier transform of a signal. In short, it computes a set of smaller FFTs (using sliding windows), computes the magnitude square of each, and averages them.
By default, \( x\) is divided into the longest possible segments to obtain as close to but not exceed eight segments with 50% overlap. Each segment is windowed with a Hamming window. The modified periodograms are averaged to obtain the PSD estimate. If you cannot divide the length of \(x\) precisely into an integer number of segments with 50% overlap, \( latex x\) is truncated accordingly.
Note the peak at 10, 20, and 30 Hz. Also, note the display default for Pwelch is in dB (logarithmic).
Let us inspect another data using the “pwelch” function of Matlab.
clear; close all; clc
load officetemp1; %16 weeks 2 samples/hr
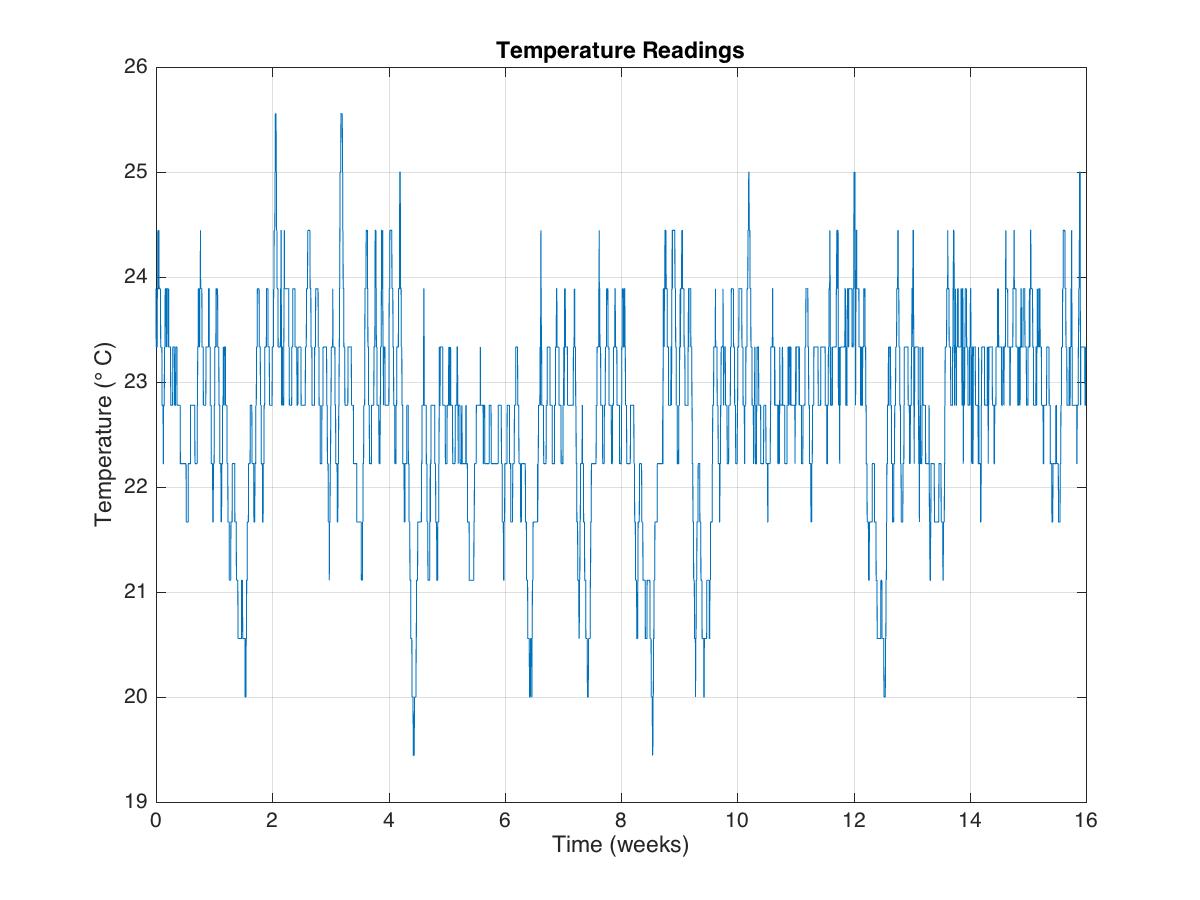
%%Visualizing data
figure(1);
plot(t,tempC)
ylabel(sprintf('Temperature (%c C)', char(176)))
xlabel('Time (weeks)')
title('Temperature Readings')
grid on
saveas(gcf,'tempReadings.jpg')
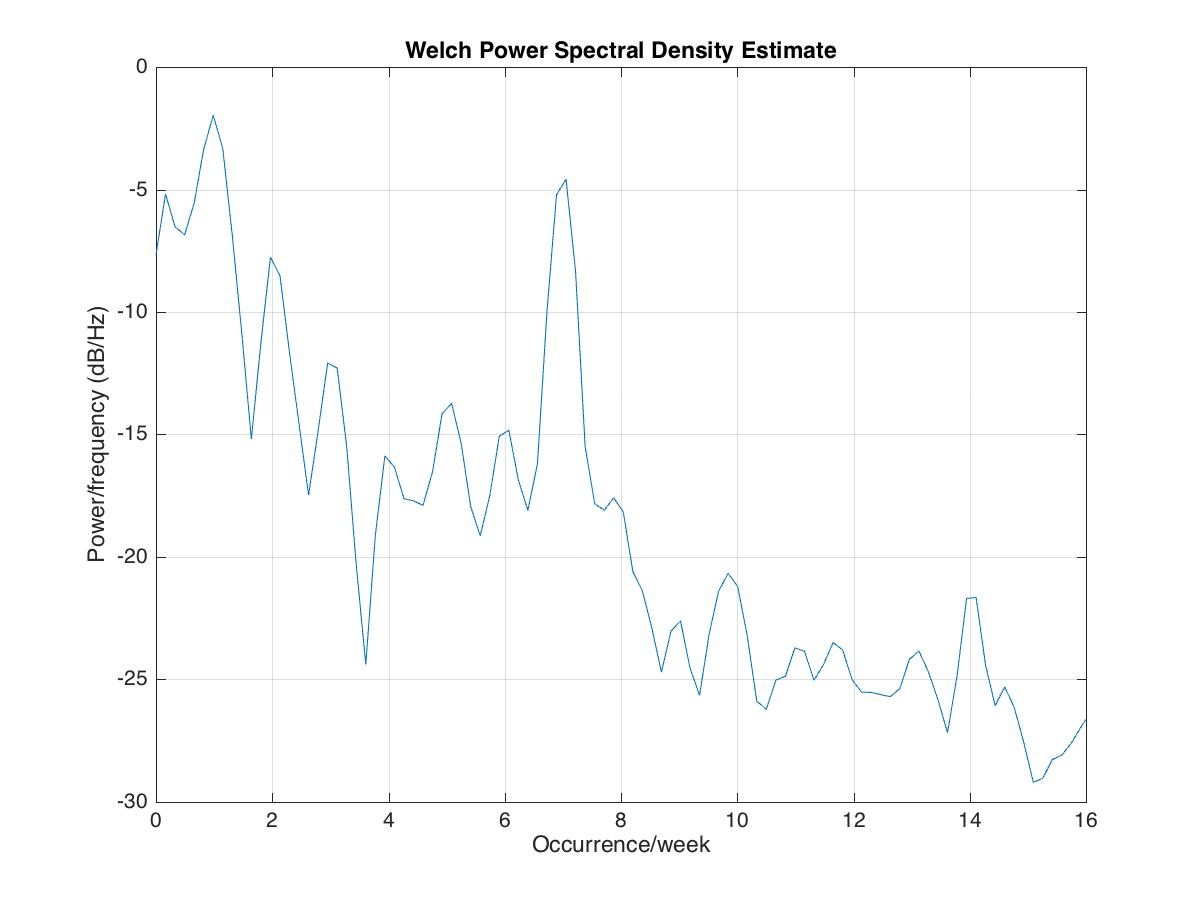
tempnorm=tempC-mean(tempC); %temperature residual
fs=2*24*7; %2 samples per hour
figure(2);
pwelch(tempnorm,[],[],[],fs);
axis([0 16 -30 0])
xlabel('Occurrence/week')
saveas(gcf,'power_spectral_tempReadings.jpg')
Resolving two close frequency components using “pwelch”
Let’s first plot the data (having the frequency components at 500 and 550 Hz) using the default parameters of the “pwelch” function:
clear; close all; clc
load winLen;
%%
pwelch(s,[],[],[],Fs);
title('pwelch with default input- f1: 500Hz, f2: 550Hz')
set(gca,'YLim',[-120,0])
set(gca,'XLim',[0,5])
saveas(gcf,'pwelchDefaultPlot.jpg')
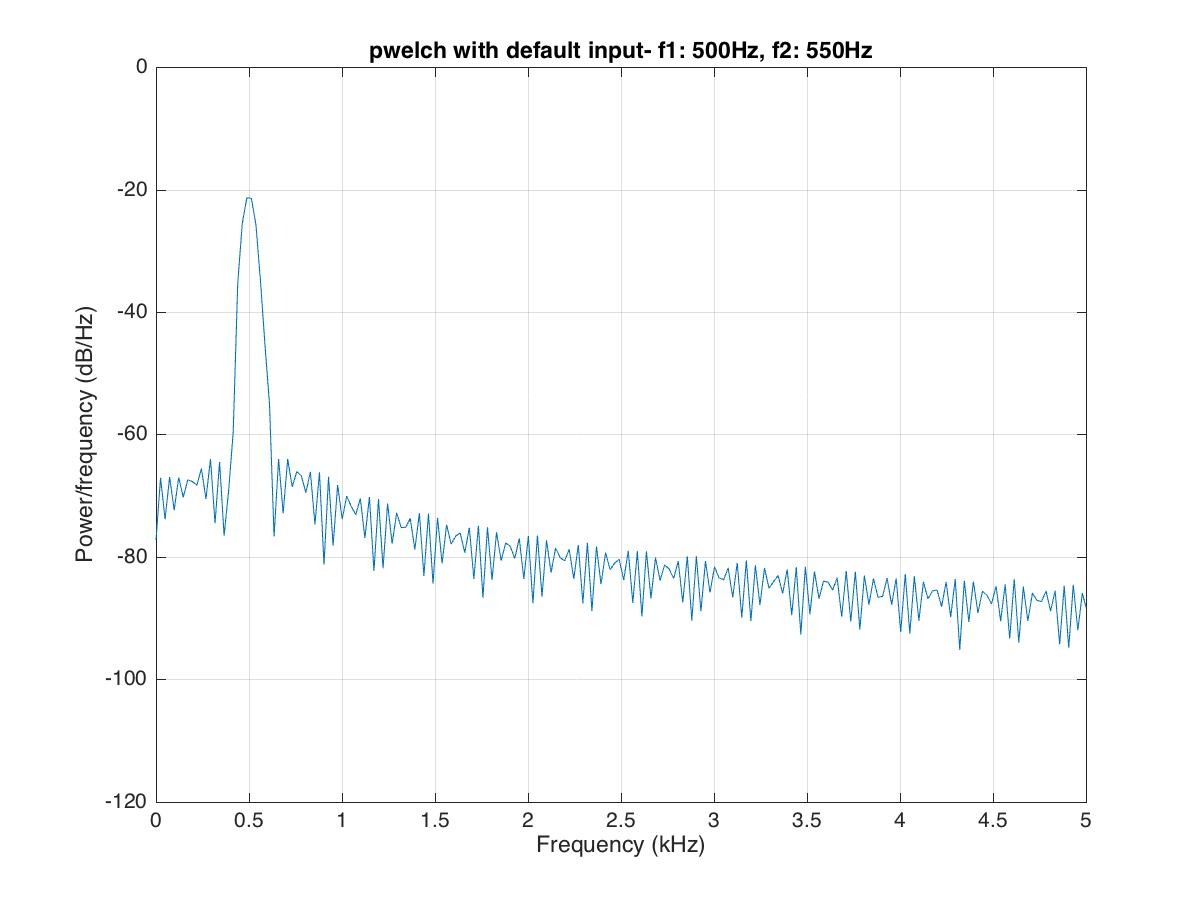
Here, we can see that the frequency component at 500Hz can be resolved, but the frequency component at 550 Hz is barely visible.
One can obtain better frequency resolution by increasing the window size:
figure;
filename = 'pwelchWindowAnalysis.gif';
for len=500:300:N
pwelch(s,len,[],len,Fs);
title(sprintf('Hamming Window size: %d',len))
set(gca,'YLim',[-120,0])
set(gca,'XLim',[0,1])
drawnow;
frame = getframe(1);
im = frame2im(frame);
[imind,cm] = rgb2ind(im,256);
if len == 500;
imwrite(imind,cm,filename,'gif', 'Loopcount',inf);
else
imwrite(imind,cm,filename,'gif','WriteMode','append');
end
end
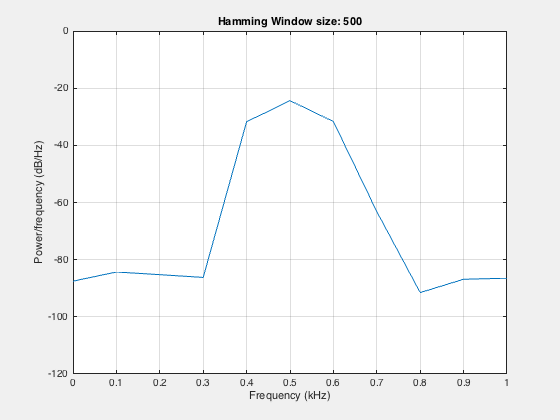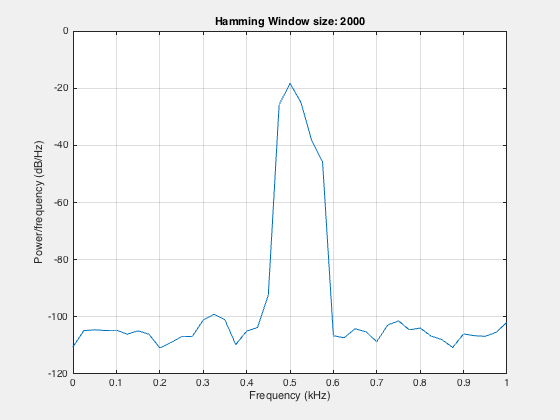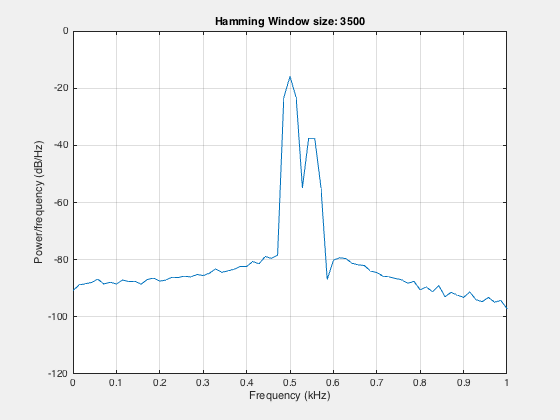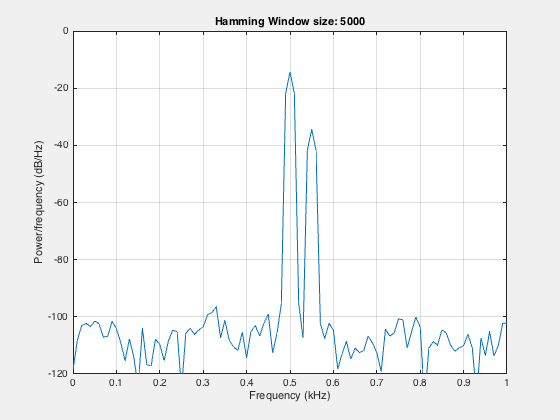
Here, we can see that by increasing the window width, we can resolve the two components. By increasing the window width, we lose the temporal resolution, but at the same time, we gain the spectral resolution.
Resolving the frequency component using the Kaiser window
The “pwelch” function uses the Hamming window by default.
L = 64;
wvtool(hamming(L))
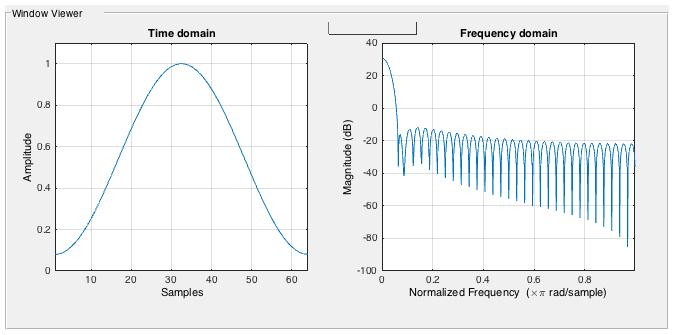
Because of the inherent property of the Hamming window (fixed side lobe), sometimes the signal can get masked.
clear; close all; clc
load winType;
figure;
pwelch(s,[],[],[],Fs);
title('pwelch with default input- f1: 500Hz, f2: 5kHz')
set(gca,'YLim',[-90,0])
set(gca,'XLim',[0,10])
saveas(gcf,'pwelchComplexDefaultPlot.jpg')
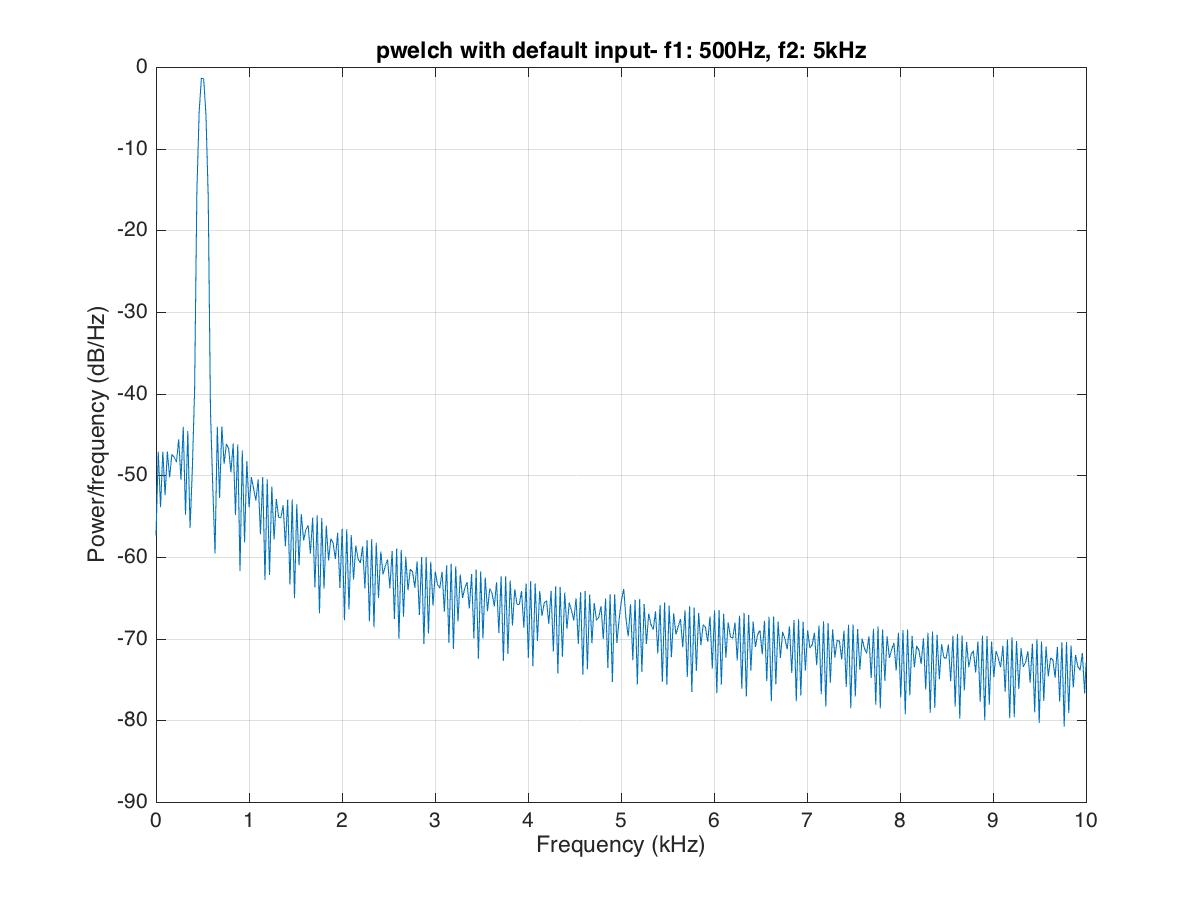
In the above figure, we can see that the signal’s frequency component at 5kHz is barely distinguishable. To resolve this component of frequency, we use the Kaiser window instead of the default Hamming window.
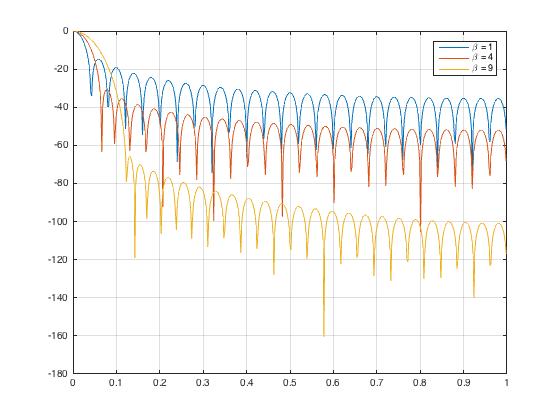
Kaiser Window in Frequency domain
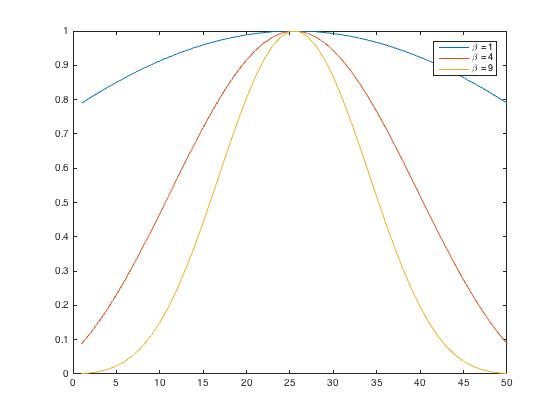
Kaiser Window in time domain
% %% Kaiser window
figure;
len=2050;
h1=kaiser(len,4.53); %side lobe attenuation of 50dB
pwelch(s,h1,[],len,Fs);
title('Kaiser window with 50dB side lobe attenuation')
saveas(gcf,'pwelchComplexKaise50dBsidelobe.jpg')
% %% Kaiser window
figure;
len=2050;
h2=kaiser(len,12.26); %side lobe attenuation of 50dB
pwelch(s,h2,[],len,Fs);
title('Kaiser window with 120dB side lobe attenuation')
saveas(gcf,'pwelchComplexKaise120dBsidelobe.jpg')
To obtain a Kaiser window that designs an FIR filter with sidelobe attenuation of α dB, we use the following β : kaiser(len,beta)
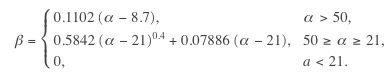
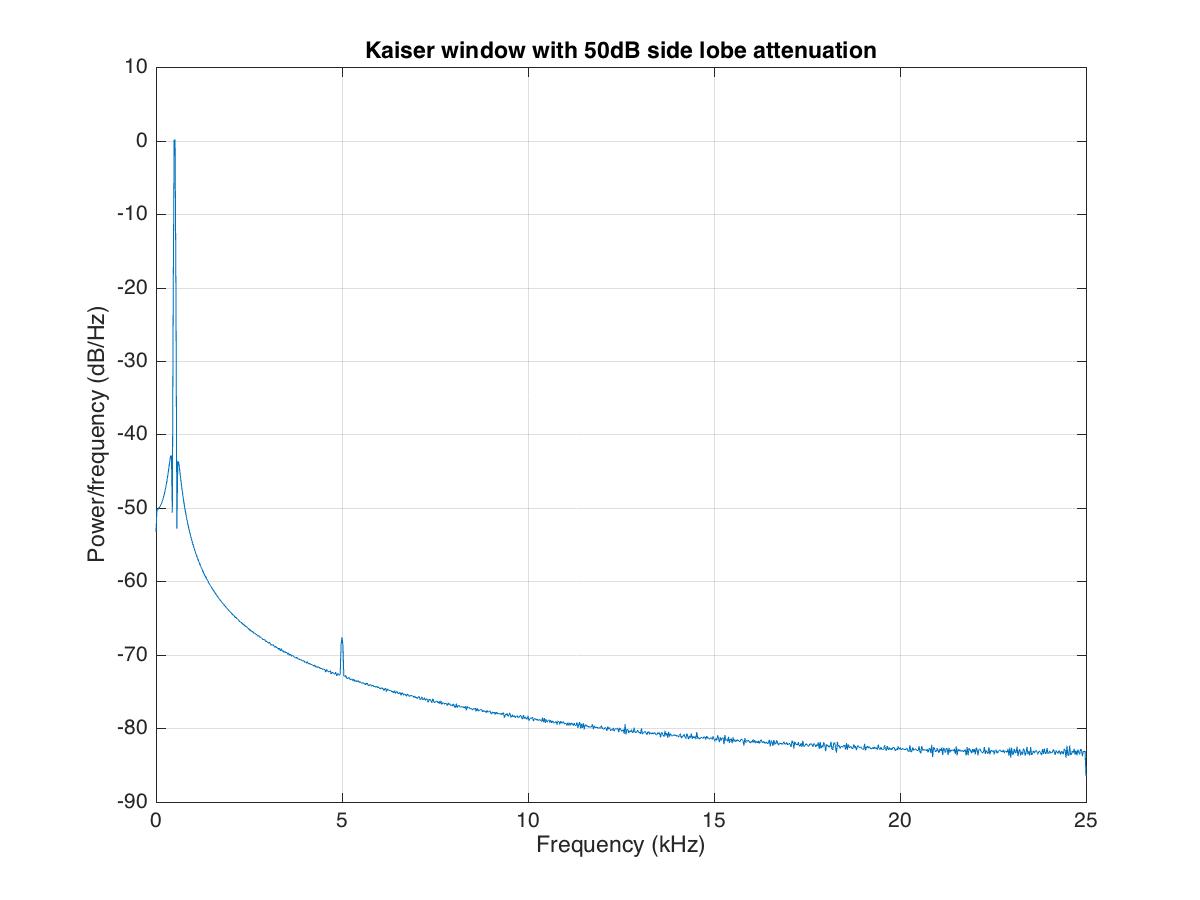
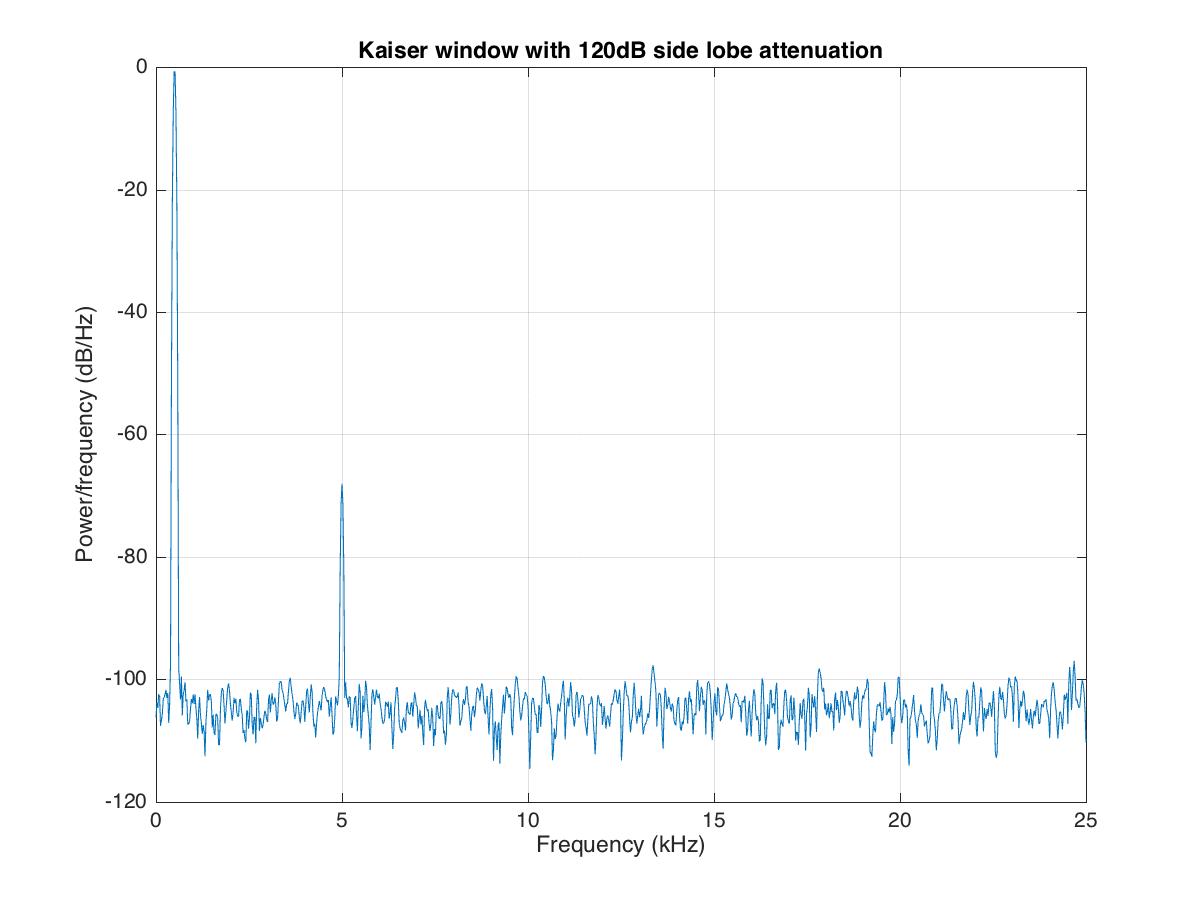
Amplitude of one frequency component is much lower than the other
We can have some signal where one frequency component’s amplitude is much lower than the others and is inundated in noise. To deal with such signals, we need to get rid of the noise using the window’s averaging.
clear; close all; clc
load winAvg;
% %% Kaiser window
figure;
len=2050;
h1=kaiser(len,4.53); %side lobe attenuation of 50dB
pwelch(s,h1,[],len,Fs);
set(gca,'XLim',[8,18]);
set(gca,'YLim',[-60,-20]);
title('Kaiser window with 50dB side lobe attenuation')
saveas(gcf,'pwelchAvgComplexKaise50dBsidelobe.jpg')
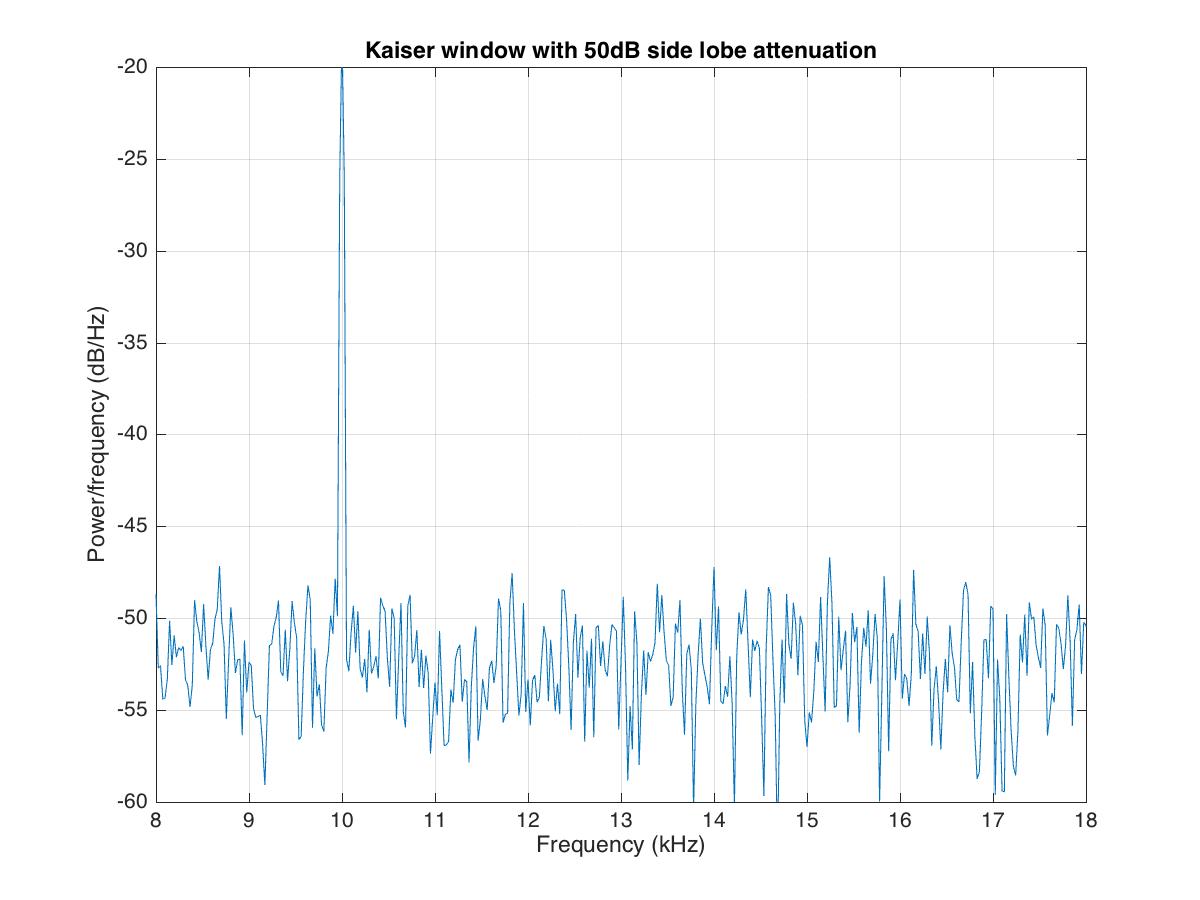
In the above signal plot, the second frequency component at 14kHz is undetectable. We can get rid of the noise using the averaging approach.
figure;
filename = 'pwelchAveraging.gif';
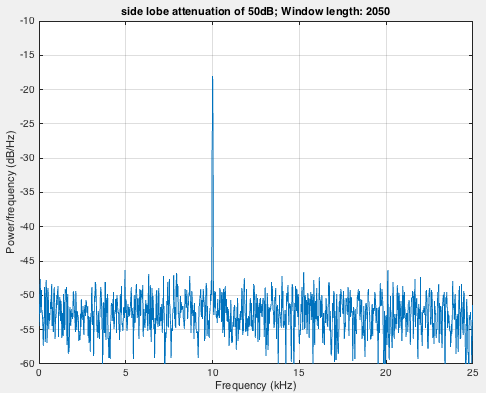
for len=2050:-100:550
h2=kaiser(len,4.53); %side lobe attenuation of 50dB
pwelch(s,h2,[],len,Fs);
drawnow;
frame = getframe(1);
im = frame2im(frame);
[imind,cm] = rgb2ind(im,256);
if len == 2050;
imwrite(imind,cm,filename,'gif', 'Loopcount',inf);
else
imwrite(imind,cm,filename,'gif','WriteMode','append');
end
end
Here, we take the smaller window in steps to show the effect of averaging. A smaller window in the frequency domain is equivalent to the larger window in the time domain.
Dealing with data having missing samples
clear; close all; clc
%%Signals having missing samples
load weightData;
plot(1:length(wgt),wgt,'LineWidth',1.2)
ylabel('Weight in kg'); xlabel('Day of the year')
grid on; axis tight; title('Weight readings of a person')
saveas(gcf,'weightReading.jpg')
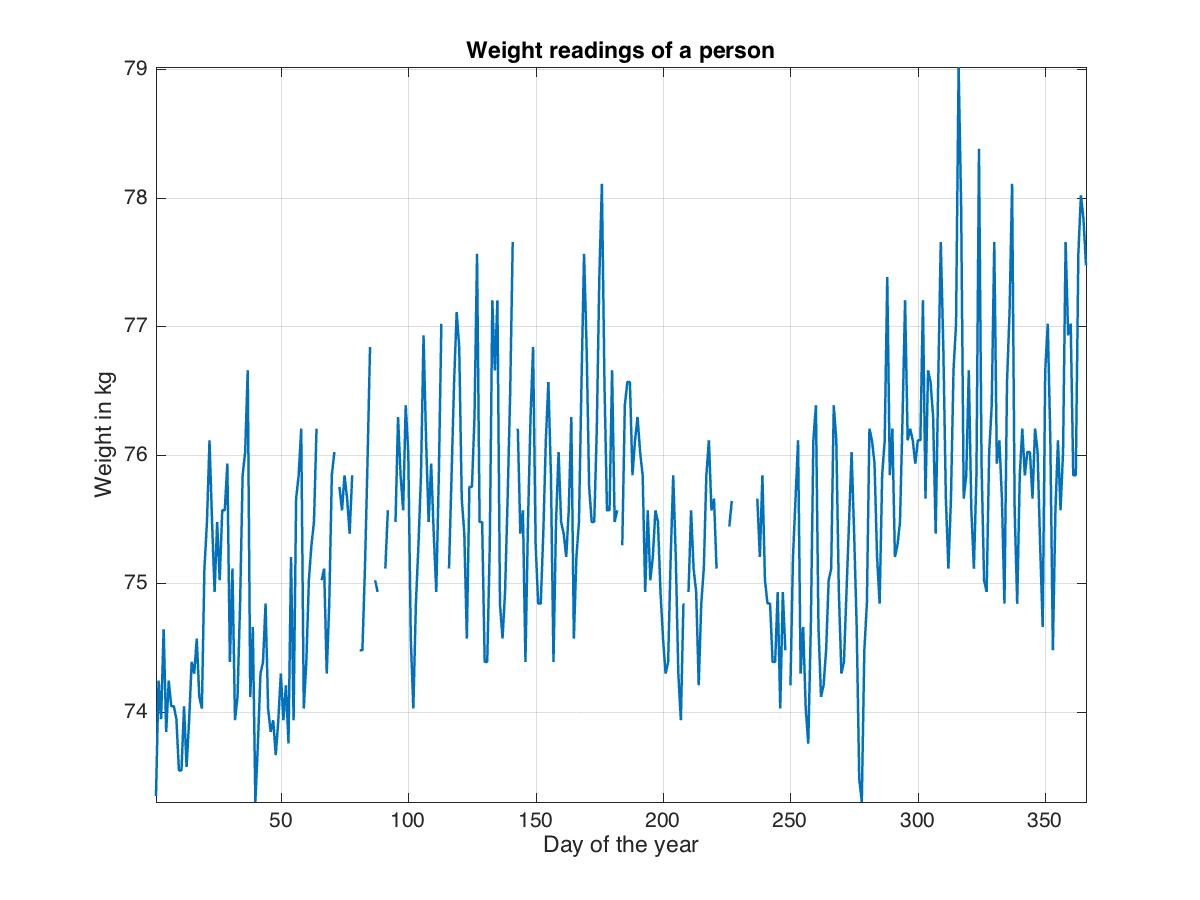
In case we have missing samples in the data, i.e., the data is not regularly recorded, then we cannot apply the “pwelch” function of Matlab to retrieve its frequency components. But thankfully, we have the function “plomb” which can be applied in such cases.
figure;
[p,f]=plomb(wgt,7,'normalized');
plot(f,p)
xlabel('Cycles per week');ylabel('Magnitude')
grid on; axis tight
saveas(gcf,'plombspectrum.jpg')
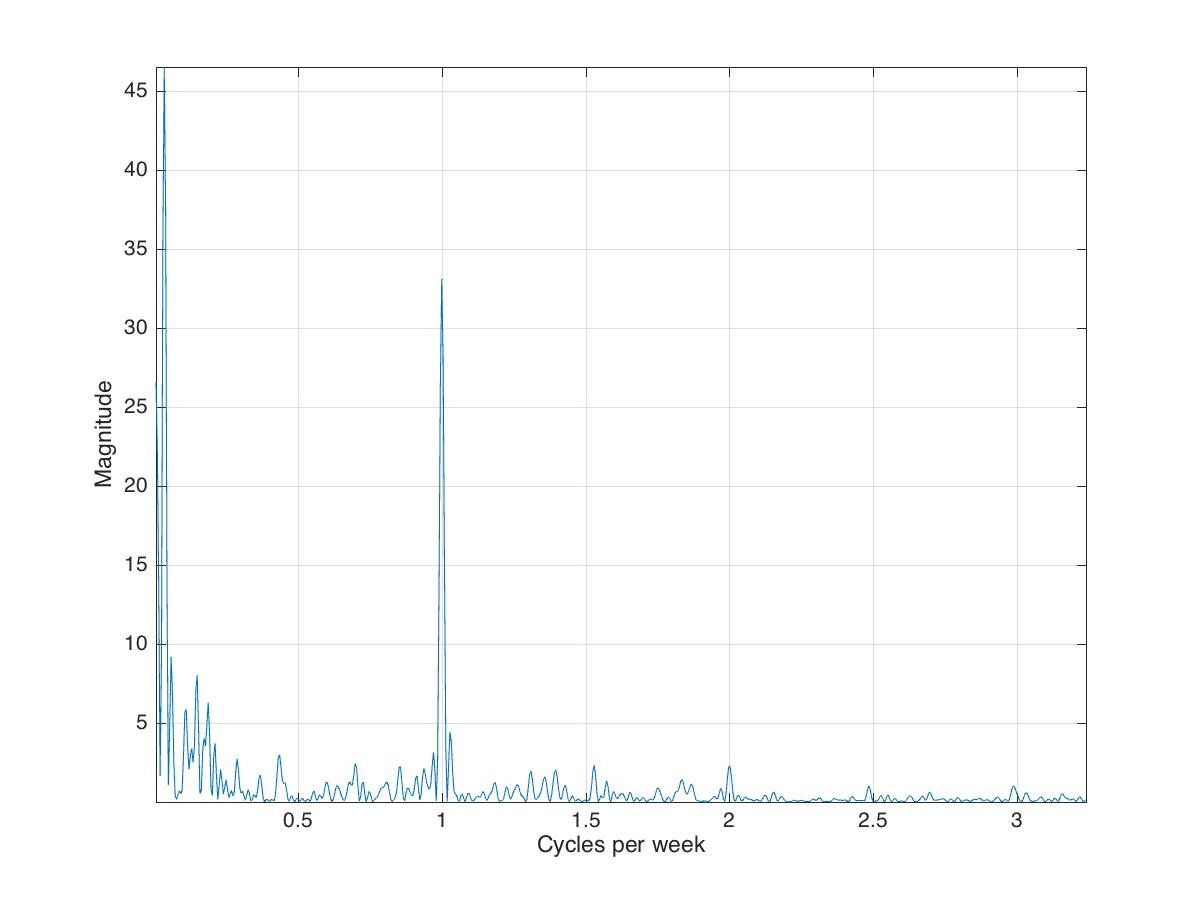
Analyzing time and frequency domain simultaneously
Sometimes, we need time and frequency information simultaneously. For a long series of data, we need to know which frequency component is recorded first and at what time. This can be done by making the spectrogram.
clear; close all; clc
load dtmf;
%%
figure;
pwelch(x,[],[],[],Fs)
saveas(gcf,'powerspectrum_dtmf.jpg')
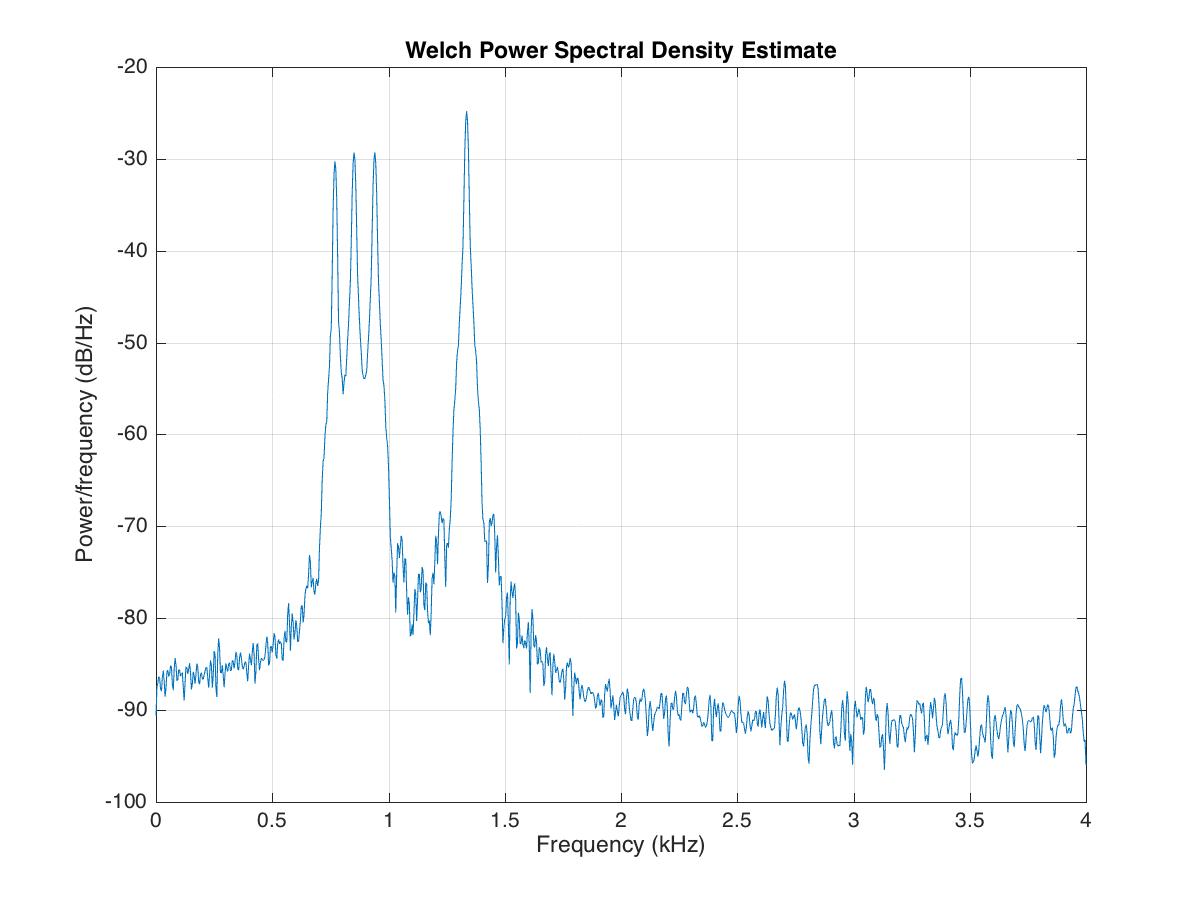
% %%
figure;
spectrogram(x,[],[],[],Fs,'yaxis'); colorbar; %default window is hamming window
saveas(gcf,'spectrogramDefault_dtmf.jpg')
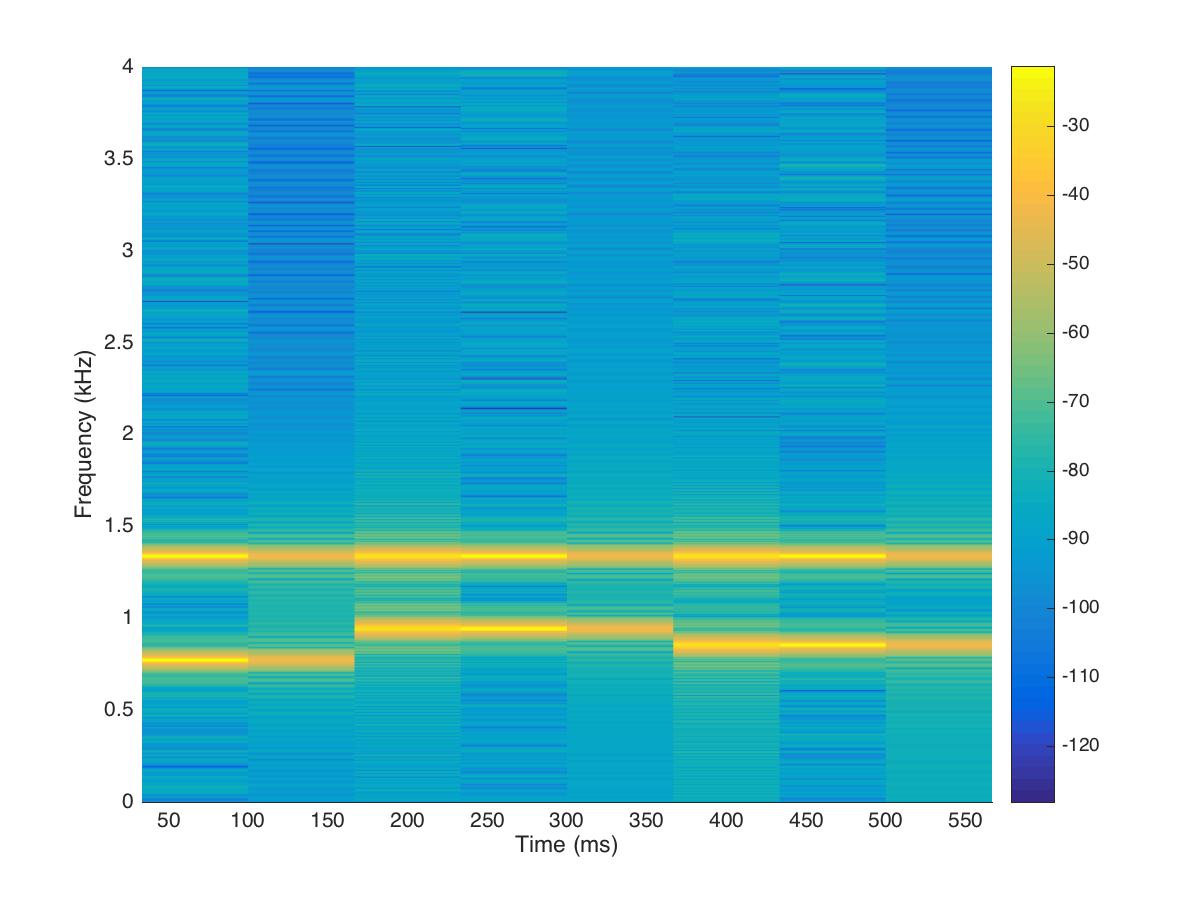
Since the time resolution is higher for smaller windows and frequency resolution is lower at small window length. So there is a trade-off between the time and frequency domain window length. We need to figure out the optimal point for better resolution in both the time and frequency domain.
segLen = [120, 240,480,600,800,1000,1200,1600];
figure;
filename='spectrogramAnalysis.gif';
for itr = 1:numel(segLen)
spectrogram(x,segLen(itr),[],segLen(itr),Fs,'yaxis');
set(gca,'YLim',[0,1.7]);
title(sprintf('window length: %d',segLen(itr)))
colorbar;
drawnow;
frame = getframe(1);
im = frame2im(frame);
[imind,cm] = rgb2ind(im,256);
if itr == 1;
imwrite(imind,cm,filename,'gif', 'Loopcount',inf);
else
imwrite(imind,cm,filename,'gif','WriteMode','append');
end
end
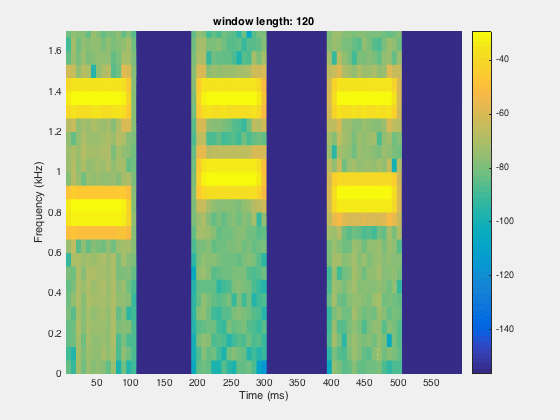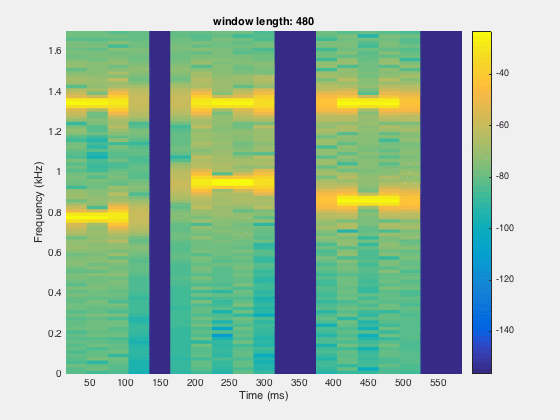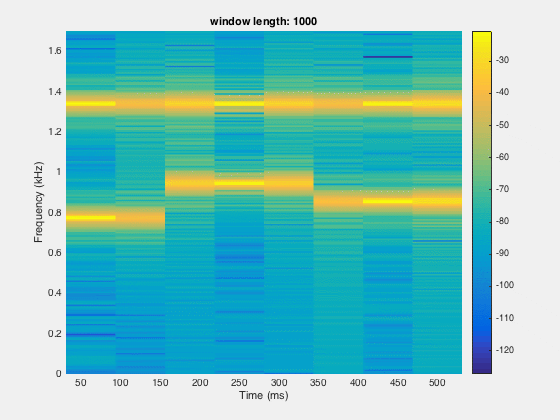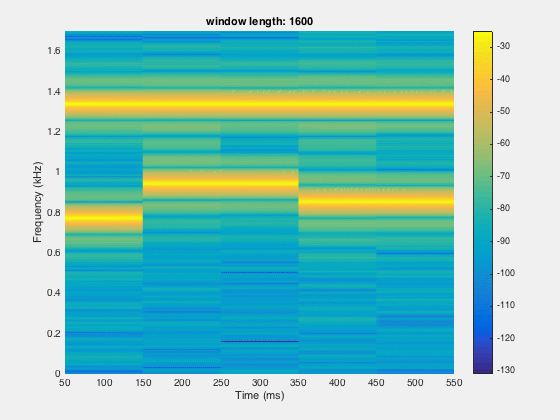
Disclaimer of liability
The information provided by the Earth Inversion is made available for educational purposes only.
Whilst we endeavor to keep the information up-to-date and correct. Earth Inversion makes no representations or warranties of any kind, express or implied about the completeness, accuracy, reliability, suitability or availability with respect to the website or the information, products, services or related graphics content on the website for any purpose.
UNDER NO CIRCUMSTANCE SHALL WE HAVE ANY LIABILITY TO YOU FOR ANY LOSS OR DAMAGE OF ANY KIND INCURRED AS A RESULT OF THE USE OF THE SITE OR RELIANCE ON ANY INFORMATION PROVIDED ON THE SITE. ANY RELIANCE YOU PLACED ON SUCH MATERIAL IS THEREFORE STRICTLY AT YOUR OWN RISK.

Leave a comment