Principal Component Analysis To Decompose Signals and Reduce Dimensionality (codes included)

Principal Component Analysis is a technique that can extract the dominant pattern in the data matrix in terms of a set of new orthogonal variables called principal components and the corresponding set of factor scores based on its dominance (e.g. Kutz 2013; Abdi & L. J. Williams 2010). Some of its applications includes data compression, image processing, exploratory data analysis, pattern recognition, time series prediction etc.

The data matrix contains the observations that are described by several inter-correlated quantitative dependent variables. The main goals of PCA are to extract the most important information (may not be most dominant) from the data matrix, compress the size of data matrix by removing orthogonal components that explains less variance for the data. The PCA computes principal components, the new set of variables, that are linear combinations of original variables. The principal components are required to have estimated variance in descending order.

Apply PCA on a time-space function

Let us apply PCA on a time-space function borrowed from Kutz (2013).

Create a function

Solutions of the form equation above are often obtained in myriad of contexts by full numerical simulations of underlying physical system.

import numpy as np
import matplotlib.pyplot as plt
from scipy import linalg
plt.style.use('seaborn')


x = np.linspace(-10,10,100)
t = np.linspace(0,10,30)

[X,T]=np.meshgrid(x,t) 

def sech(X):
    return 1/np.cosh(X)

f=sech(X)*(1-0.5*np.cos(2*T))+(sech(X)*np.tanh(X))*(1-0.5*np.sin(2*T))


vmin = np.amin(f)
vmax = np.amax(f)


from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=plt.figaspect(0.8))
ax = fig.gca(projection='3d')
# Plot the surface.
surf = ax.plot_surface(T, X, f, cmap='summer',linewidth=0, antialiased=True, rstride=1, cstride=1, alpha=None)
ax.set_ylabel(r'$X$')
ax.set_xlabel(r'$T$')
surf.set_clim(vmin,vmax)
plt.colorbar(surf)
plt.tight_layout()
plt.savefig('PCA_space_time_func.png',dpi=300,bbox_inches='tight')
plt.close('all')

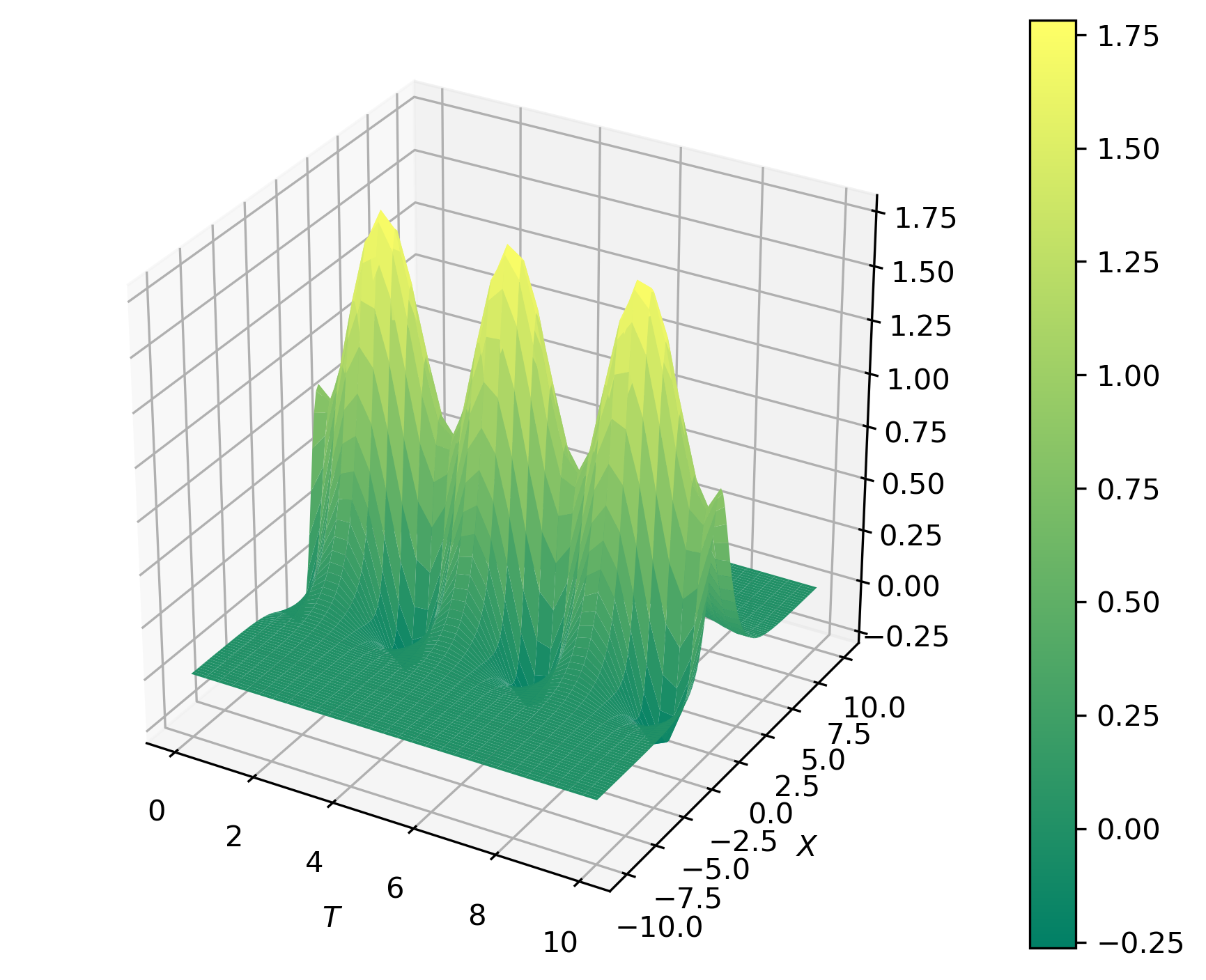
Compute the PCA

We can apply PCA to investigate the dynamics of this system.

u,s,v = linalg.svd(f, full_matrices=False,check_finite=False)
eigen_values = s
s = np.diag(s)

pca_modes = []
for j in range(1,3):
    ff=u[:,0:j].dot(s[0:j,0:j]).dot(v[0:j,:])
    pca_modes.append(ff)


vmin = np.min([np.amin(pca_modes[0]),np.amin(pca_modes[1])])
vmax = np.max([np.amax(pca_modes[0]),np.amax(pca_modes[1])])

Plot the Spatial Pattern

## Spatial behaviour
fig = plt.figure(figsize=plt.figaspect(0.5))
for jj in range(len(pca_modes)):
    ax = fig.add_subplot(1, 2, jj+1, projection='3d')
    surf = ax.plot_surface(T, X, pca_modes[jj], cmap='summer',linewidth=0, antialiased=True, rstride=1, cstride=1, alpha=None)
    surf.set_clim(vmin,vmax)
    ax.set_ylabel(r'$X$')
    ax.set_xlabel(r'$T$')
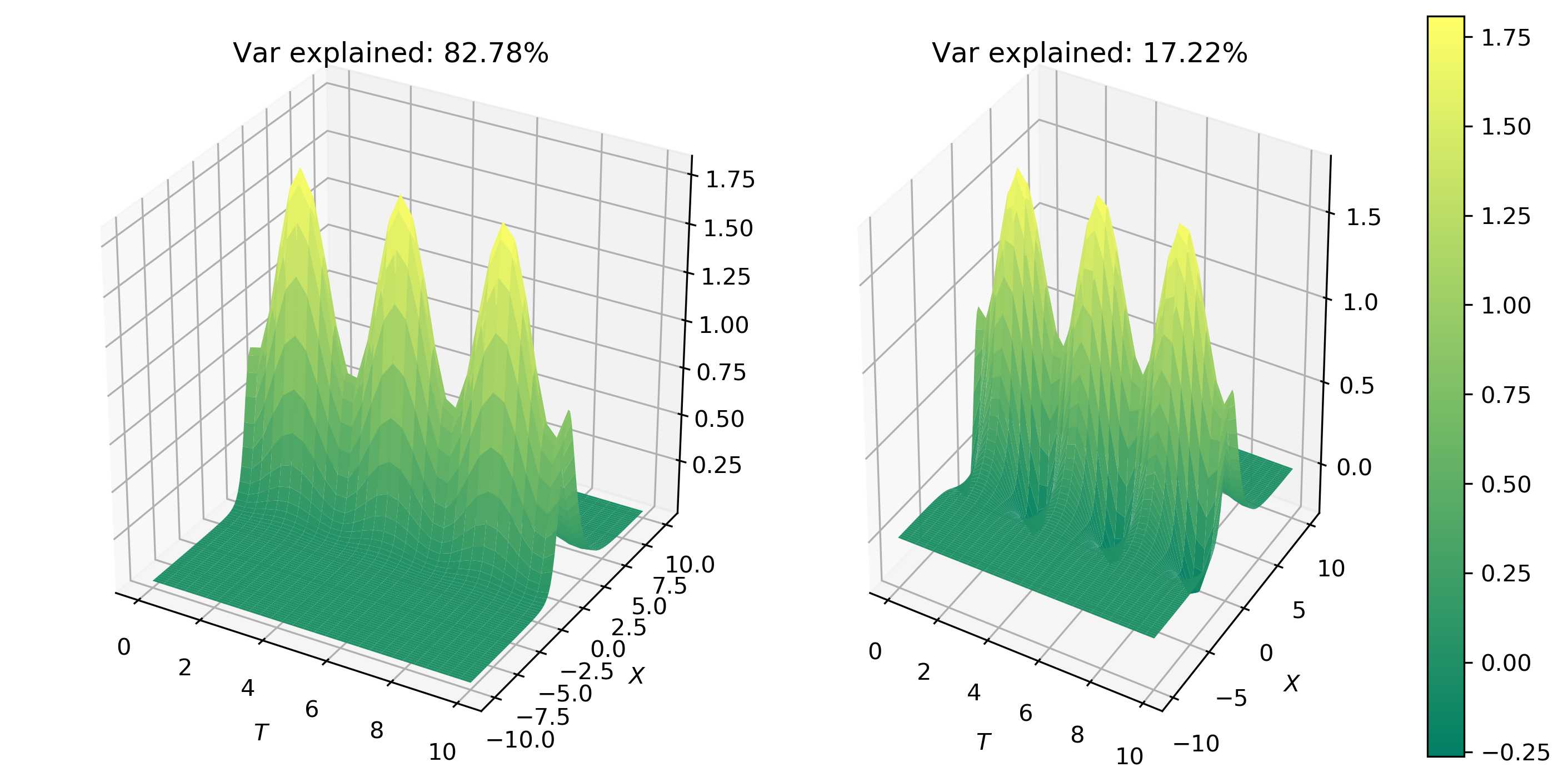
    ax.set_title('Var explained: {:.2f}%'.format(eigen_values[jj]/np.sum(eigen_values)*100))

plt.colorbar(surf)
plt.subplots_adjust(hspace=0.5,wspace=0.05)
plt.tight_layout()
plt.savefig('PCA_space_time_func_modes.png',dpi=300,bbox_inches='tight')
plt.close('all')

The first two modes capture 100% of the total surface energy in the system. Hence, the third mode is completely unnecessary. This suggests that system can be easily and accurately represented by a simple two-mode expansion.

Figure 2 shows the spatial behavior of the first two modes.

Plot the temporal pattern

## temporal behaviour
fig, ax = plt.subplots(2,1,figsize=plt.figaspect(0.5))
ax[0].plot(x,v[0,:],'k-',label='mode 1')
ax[0].plot(x,v[1,:],'k--',label='mode 2')
ax[0].set_xlabel('x')
ax[0].set_ylabel('PCA modes')
ax[0].legend()


ax[1].plot(t,u[:,0],'k-',label='mode 1')
ax[1].plot(t,u[:,1],'k--',label='mode 2')
ax[1].set_xlabel('x')
ax[1].set_ylabel('PCA modes')
ax[1].legend()

plt.subplots_adjust(hspace=0.5,wspace=0.05)
plt.tight_layout()
plt.savefig('PCA_space_time_behaviour.png',dpi=300,bbox_inches='tight')
plt.close('all')

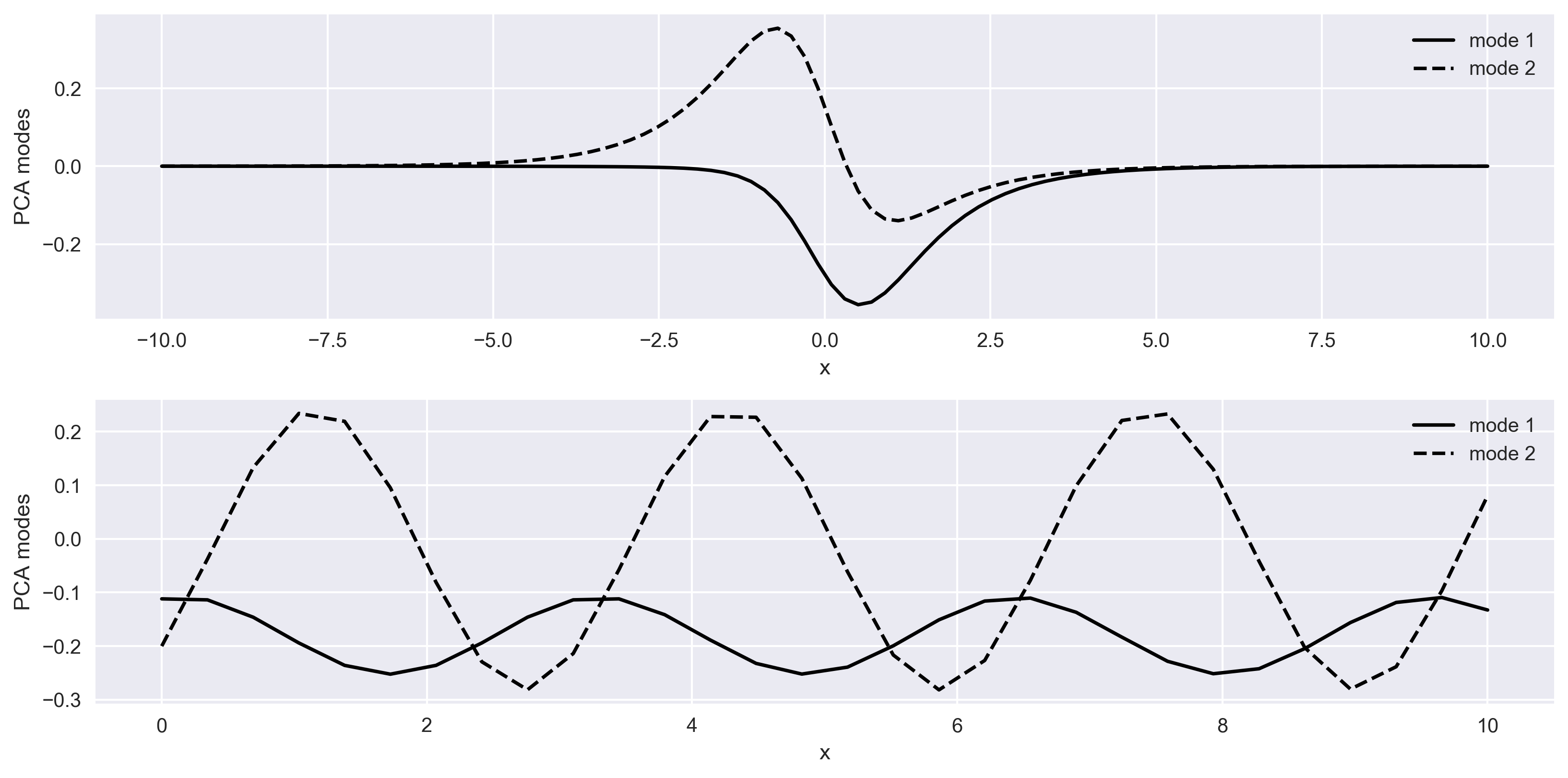
In Figure 3, top panel shows the spatial behaviour of the system for the two modes, and bottom panel shows the temporal evolution of the system for two modes.

Complete Code

Recap

• PCA = new axes along maximum variance. The principal components are orthogonal directions ranked by how much of the data’s spread they capture.
• SVD does it in one line. u, s, v = svd(f) gives the modes; a truncated product u[:,:j] s[:j,:j] v[:j,:] reconstructs the signal from the top-$j$ modes.
• Few modes, most of the signal. Here two modes captured 100% of the energy, so the field compresses to a two-mode expansion with no loss.
• Variance uses squared singular values. The exact percentage is $s_i^2 / \sum s_j^2$.
• Same math as EOF. Run this on a space–time field and PCA is EOF analysis.

Where to go next

• EOF analysis (PCA on a space–time field): Empirical Orthogonal Function analysis
• numpy.linalg.svd docs: numpy.org/doc/stable/reference/generated/numpy.linalg.svd.html
• sklearn.decomposition.PCA (a batteries-included API): scikit-learn.org — PCA

References

1. Principal component analysis — Abdi, H., & Williams, L. J., 2010, Wiley Interdisciplinary Reviews: Computational Statistics, 2(4), 433–459.
2. Kutz, J. N. (2013). Data-driven modeling & scientific computation: methods for complex systems & big data. Oxford University Press.