Solving boundary value problems using the shooting method
The boundary value problems require information at the present time and a future time. We will see how we can use shooting method to solve problems where we have the boundary constraints.
We have done several posts on the numerical problems such as using Euler method or Runge-Kutta methods for which the initial conditions are known. However, many physical applications do not have specified initial conditions, but rather some given boundary (constraint) conditions. The boundary value problems require information at the present time \((t = a)\) and a future time \((t = b)\). However, the time-stepping schemes developed previously in the case of initial value problems only require information about the starting time \(t = a\). In this post, we will see a quick and easy way to solve these boundary value problems.
Similar posts
The Shooting Method
Let us begin by considering the generic boundary value problem:
\begin{equation} \frac{d^2\vec{y}}{dt^2} = f(t,\vec{y},\frac{d\vec{y}}{dt}) \end{equation}
on \(t \in [a, b]\) with the boundary conditions
\begin{equation} y(a) = \alpha \end{equation}
\begin{equation} y(b) = \beta \end{equation}
The stepping schemes considered thus far for second-order differential equations involve a choice of the initial conditions \(y(a)\) and \(y’(a)\). If we want to solve the above problem in a initial value problem approach, we can rewrite the above differential equation as below.
\begin{equation} \frac{dy}{dt} = z \end{equation}
For this equation, we need \(y(a) = \alpha\), which is known.
\begin{equation} \frac{dz}{dt} = f(t,\vec{y},\frac{d\vec{y}}{dt}) \end{equation} For this equation, we need \(z(a) = \kappa\), where \(\kappa\) is unknown. Our goal here is to determine the value of \(\kappa\) with the constrain \(y(b) = \beta\).
For this, we can define a function \(F = F(\kappa)\): \begin{equation} F(\kappa) = y(b) - \beta \end{equation} We have to find \(\kappa\) such that \(F(\kappa)=0\). This becomes a root finding problem and we know how to solve these problems (see Newton–Raphson method).
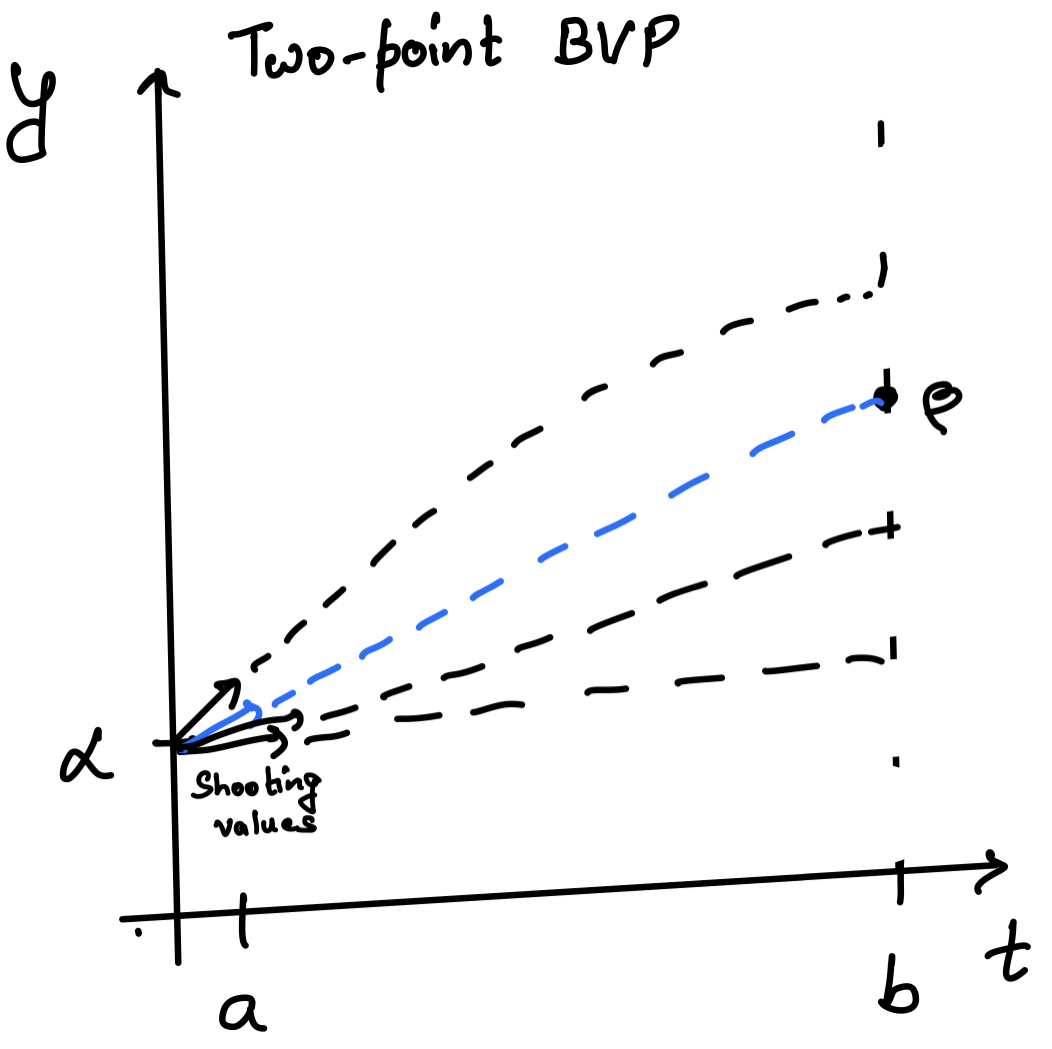
The value of \(\kappa\) is the slope of the y function at \(t=a\).
The shooting method gives a procedure to iteratively determine this constant A. In other words, we will be applying our modified initial value problem approach (the Runge-Kutta method) to solve the boundary value problems.
Example 1
Let us start with a very simple problem of freefall of a ball under the effect of gravity.
\begin{equation} \frac{d^2\vec{y}}{dt^2} = -g \end{equation} where, \(g=9.8\)m/s^2. The boundary condition here is that we start at \(y=0\) with unknown velocity, but we know that it will be back at \(t=10\).
import numpy as np
from scipy.integrate import solve_ivp
from scipy import optimize
import matplotlib.pyplot as plt
plt.style.use('seaborn')
g = 9.8
y0 = 0
tf = 10
def f(t, r):
y, v = r
dy_dt = v # velocity
d2y_dt2 = -g # acceleration
return dy_dt, d2y_dt2
@np.vectorize
def shooting_eval(v0):
sol = solve_ivp(f, (t[0], t[-1]), (y0, v0), t_eval=t)
y_num, v = sol.y
return y_num[-1]
v0 = 60 # guess the initial velocity
t = np.linspace(0, tf, 51)
fig, ax = plt.subplots()
v0 = np.linspace(0, 100, 100)
plt.plot(v0, shooting_eval(v0), label='Shooting evaluation')
plt.axhline(c="k")
# root finding: secant method (kind of Newton Raphson method where slope is unknown)
# Find a zero of the function func given a nearby starting point x0
v0 = optimize.newton(shooting_eval, 50)
print(v0)
plt.plot(v0, 0, 'ro', label=f'Solution: {v0:.1f}')
plt.grid(True)
plt.legend()
ax.set_xlabel('t')
ax.set_ylabel('y')
plt.savefig('example1_solution.png', bbox_inches='tight', dpi=300)
plt.close()
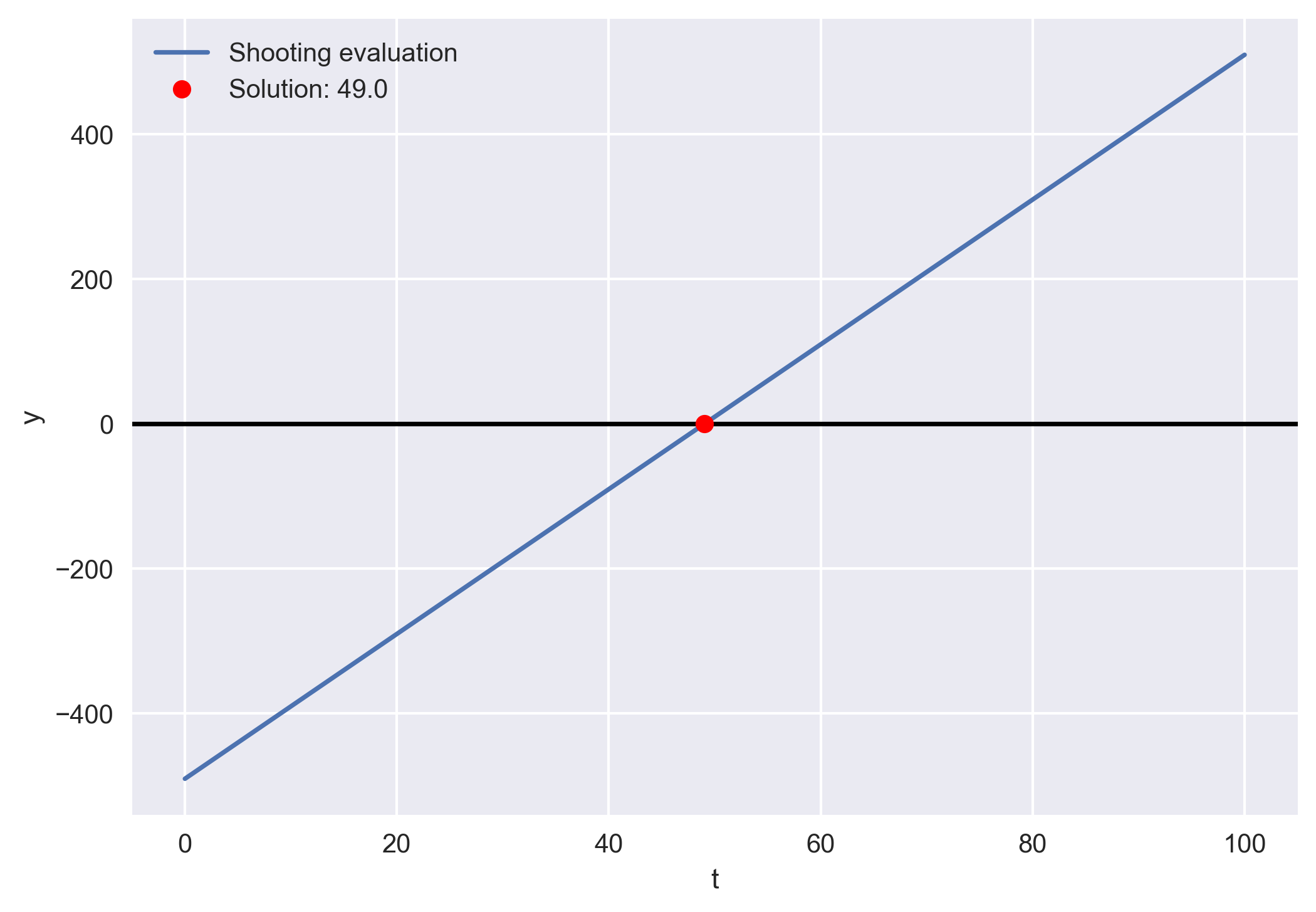
Here, we found the initial velocity to be 49.0 m/s.
# Plot the path
t = np. linspace(0, tf, 51)
sol = solve_ivp(f, (0, tf), (y0, v0), t_eval=t)
y, v = sol.y
plt.plot(t[0], y0, 'ro', label=f'Solution: {v0:.1f}')
plt.plot(t[-1], 0, 'ro', label=f'Solution: {v0:.1f}')
plt.plot(t, y, ".")
plt.savefig('example1_solution_path.png', bbox_inches='tight', dpi=300)
plt.close()
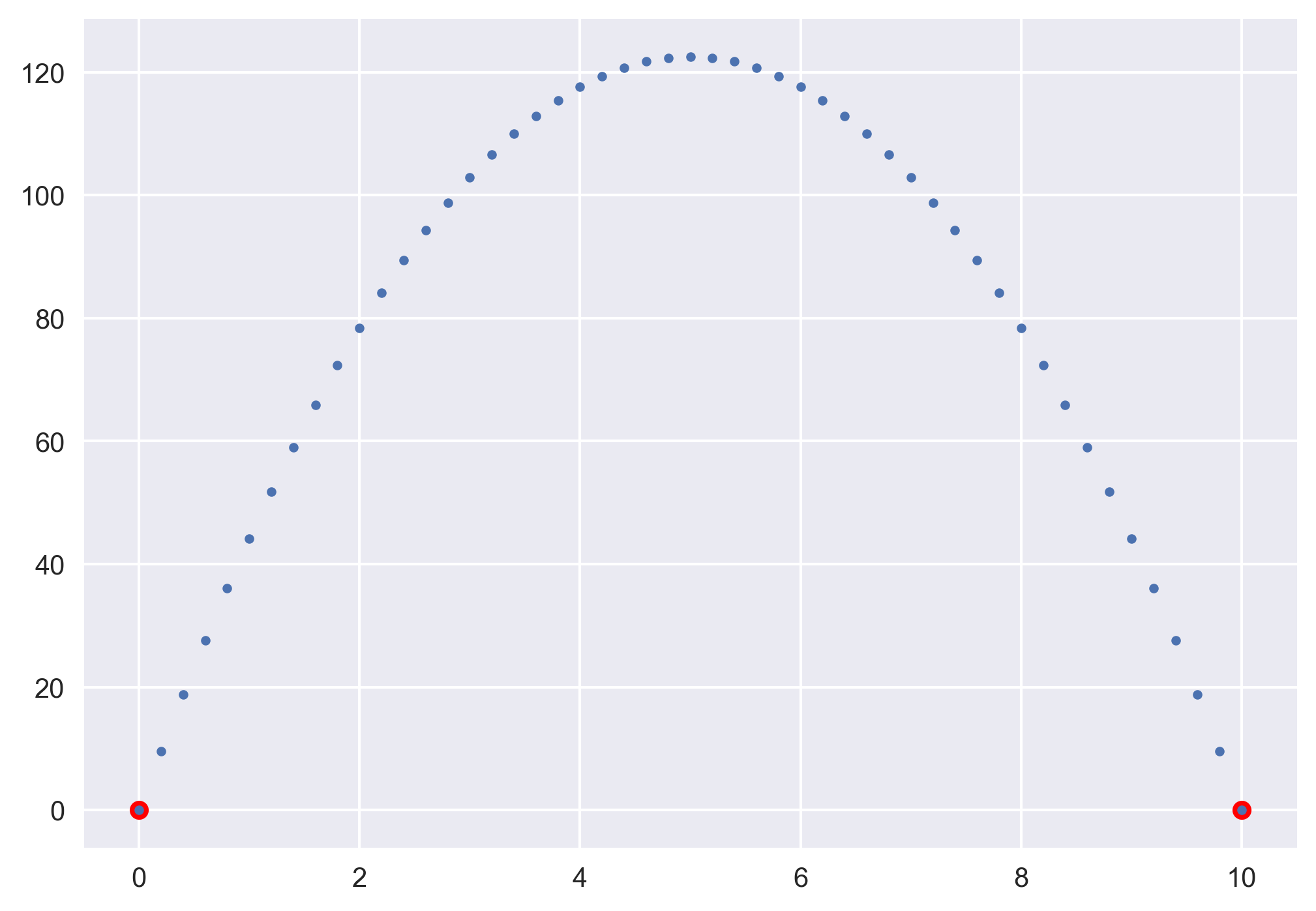
Example 2
Let us take another simple differential equation to solve.
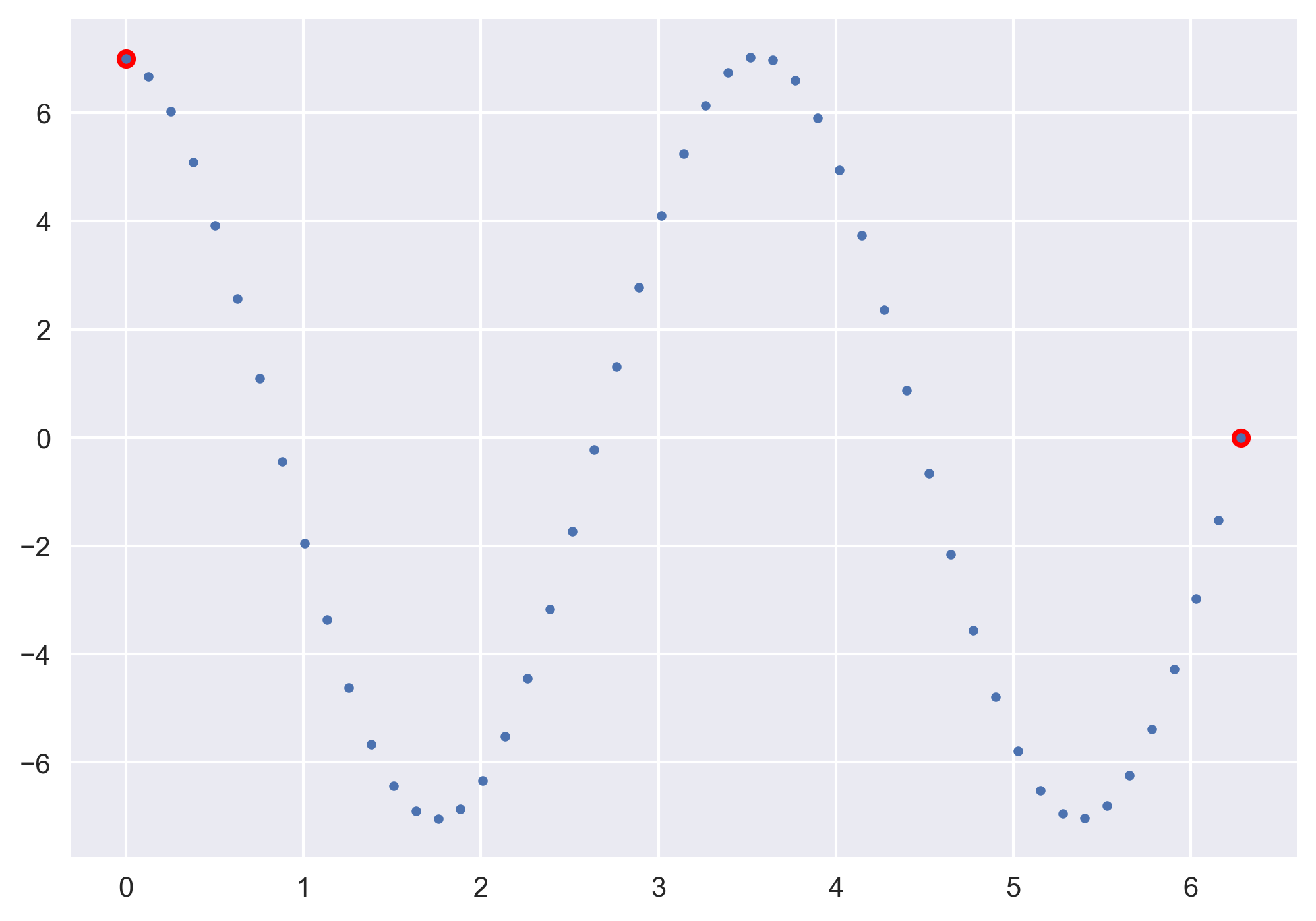
\begin{equation} \frac{d^2\vec{y}}{dt^2} +3y = 0 \end{equation} where, \(y(0) = 7\) and \(y(2*\pi)=0\).
import numpy as np
from scipy.integrate import solve_ivp
from scipy import optimize
import matplotlib.pyplot as plt
plt.style.use('seaborn')
# example d2y/dt2+3y = 0
# y(0) = 7 and y(2*pi)=0
y0 = 7
tf = 2 * np.pi
def f(t, r):
y, v = r
dy_dt = v # velocity
d2y_dt2 = -3 * y # acceleration
return dy_dt, d2y_dt2
@np.vectorize
def shooting_eval(v0):
sol = solve_ivp(f, (t[0], t[-1]), (y0, v0), t_eval=t)
y_num, v = sol.y
return y_num[-1]
v0 = 60 # guess the initial velocity
t = np.linspace(0, 2 * np.pi, 100)
fig, ax = plt.subplots()
v0 = np.linspace(0, 100, 100)
plt.plot(v0, shooting_eval(v0), label='Shooting evaluation')
plt.axhline(c="k")
# root finding: secant method (kind of Newton Raphson method where slope is unknown)
# Find a zero of the function func given a nearby starting point x0
v0 = optimize.newton(shooting_eval, 50)
print(v0)
plt.plot(v0, 0, 'ro', label=f'Solution: {v0:.1f}')
plt.grid(True)
plt.legend()
ax.set_xlabel('t')
ax.set_ylabel('y')
plt.savefig('example2_solution.png', bbox_inches='tight', dpi=300)
plt.close()
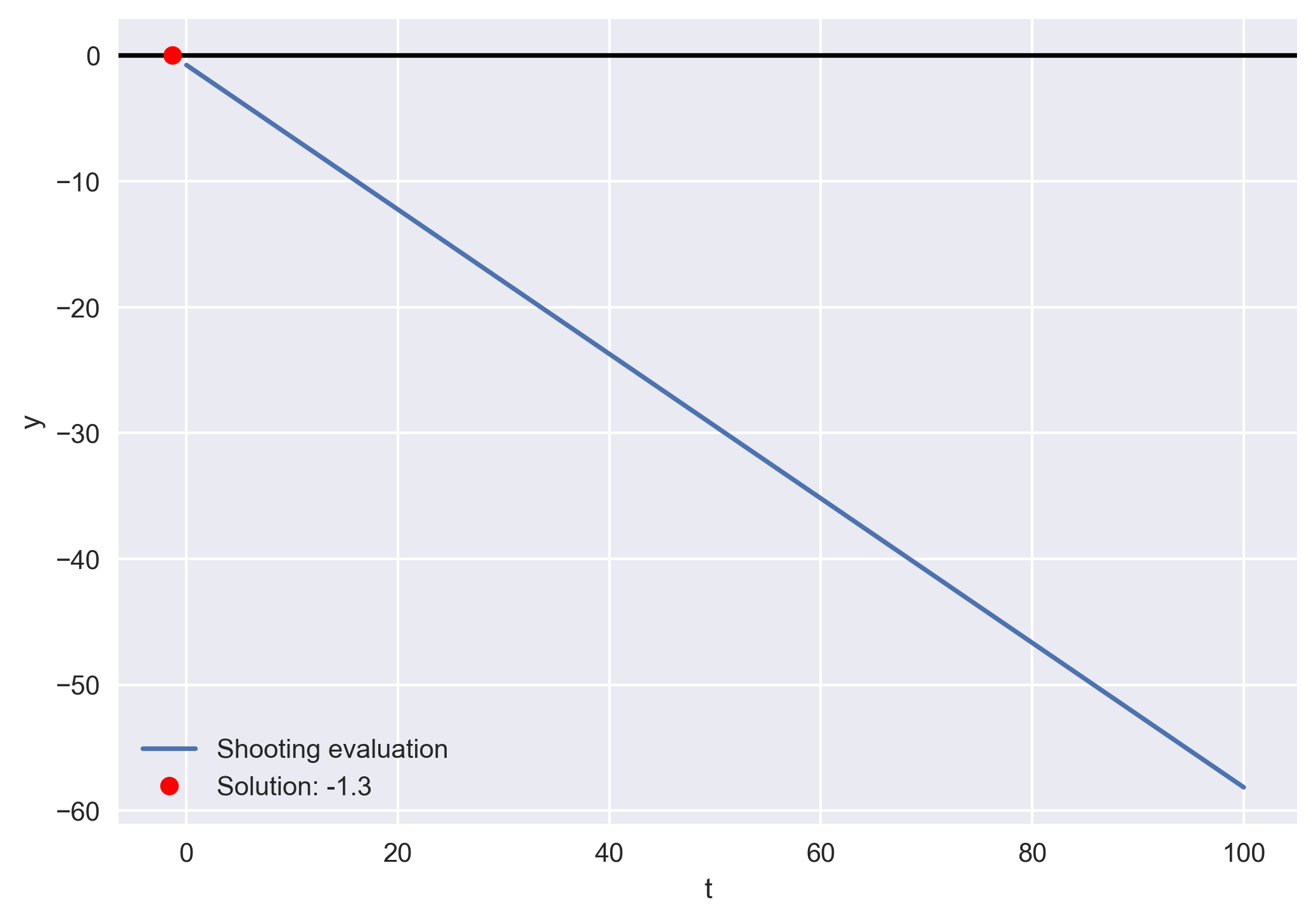
# Plot the path
t = np. linspace(0, tf, 51)
sol = solve_ivp(f, (0, tf), (y0, v0), t_eval=t)
y, v = sol.y
plt.plot(t[0], y0, 'ro', label=f'Solution: {v0:.1f}')
plt.plot(t[-1], 0, 'ro', label=f'Solution: {v0:.1f}')
plt.plot(t, y, ".")
plt.savefig('example2_solution_path.png', bbox_inches='tight', dpi=300)
plt.close()
References
- Kutz, J. N. (2013). Data-driven modeling & scientific computation: methods for complex systems & big data. Oxford University Press.
Disclaimer of liability
The information provided by the Earth Inversion is made available for educational purposes only.
Whilst we endeavor to keep the information up-to-date and correct. Earth Inversion makes no representations or warranties of any kind, express or implied about the completeness, accuracy, reliability, suitability or availability with respect to the website or the information, products, services or related graphics content on the website for any purpose.
UNDER NO CIRCUMSTANCE SHALL WE HAVE ANY LIABILITY TO YOU FOR ANY LOSS OR DAMAGE OF ANY KIND INCURRED AS A RESULT OF THE USE OF THE SITE OR RELIANCE ON ANY INFORMATION PROVIDED ON THE SITE. ANY RELIANCE YOU PLACED ON SUCH MATERIAL IS THEREFORE STRICTLY AT YOUR OWN RISK.

Leave a comment